Pohyb funkčných grafov. Konverzia funkčných grafov

Späť Vpred

Pozor! Ukážky snímok slúžia len na informačné účely a nemusia predstavovať všetky funkcie prezentácie. Ak vás táto práca zaujala, stiahnite si plnú verziu.

Cieľ lekcie: Určte vzory transformácie funkčných grafov.

Úlohy:

Vzdelávacie:

• Naučte študentov zostavovať grafy funkcií transformáciou grafu danej funkcie, pomocou paralelného prekladu, kompresie (natiahnutia) a rôznych typov symetrie.

Vzdelávacie:

• Kultivovať osobné vlastnosti žiakov (schopnosť počúvať), dobrú vôľu k iným, pozornosť, presnosť, disciplínu a schopnosť pracovať v skupine.
• Pestovať záujem o predmet a potrebu získavať vedomosti.

vývojové:

• Rozvíjať priestorovú predstavivosť a logické myslenie žiakov, schopnosť rýchlej orientácie v prostredí; rozvíjať inteligenciu, vynaliezavosť a trénovať pamäť.

Vybavenie:

• Multimediálna inštalácia: počítač, projektor.

Literatúra:

1. Bashmakov, M. I. Matematika [Text]: učebnica pre inštitúcie zač. a streda Prednášal prof. vzdelanie / M.I. Bashmakov - 5. vyd. – M.: Edičné stredisko „Akadémia“, 2012. – 256 s.
2. Bašmakov, M. I. Matematika. Problémová kniha [Text]: učebnica.

príspevok na vzdelanie inštitúcie skoro a streda

1. Prednášal prof. vzdelávanie / M. I. Bashmakov – M.: Edičné centrum „Akadémia“, 2012. – 416 s.
2. Plán lekcie:
3. Organizačný moment (3 min).
4. Aktualizácia vedomostí (7 min).
5. Vysvetlenie nového materiálu (20 min).
6. Spevnenie nového materiálu (10 min).

Zhrnutie lekcie (3 min).

Domáca úloha (2 min).

Pokrok v lekcii

1. Org. moment (3 minúty).

Kontrola prítomných.

Komunikujte účel lekcie.

Skôr než si povieme niečo o grafových transformáciách, zopakujme si materiál, ktorý sme prebrali.

Ústna práca. (Snímka 2).

Poskytnuté funkcie:

3. Opíšte grafy funkcií: , , , .

3. Vysvetlenie nového materiálu (20 min).

Najjednoduchšie transformácie grafov sú ich paralelný prenos, kompresia (natiahnutie) a niektoré typy symetrie. Niektoré transformácie sú uvedené v tabuľke (Príloha 1), (Snímka 3).

Pracujte v skupinách.

Každá skupina vytvorí grafy daných funkcií a predloží výsledok na diskusiu.

Funkcia	Transformácia grafu funkcie	Príklady funkcií	Snímka
	Oh na A jednotky až ak A>0 a na |A| jednotky dole ak A<0.	,	(Snímka 4)
	Paralelný prenos pozdĺž osi Oh na A jednotky doprava ak A>0 a ďalej - A jednotky doľava ak A<0.	,	(Snímka 5)

Základné elementárne funkcie v čistej forme bez transformácie sú zriedkavé, takže najčastejšie musíte pracovať s elementárnymi funkciami, ktoré boli získané z hlavných sčítaním konštánt a koeficientov. Takéto grafy sú konštruované pomocou geometrických transformácií daných elementárnych funkcií.

Uvažujme príklad kvadratickej funkcie tvaru y = - 1 3 x + 2 3 2 + 2, ktorej grafom je parabola y = x 2, ktorá je trikrát stlačená vzhľadom na Oy a symetrická vzhľadom na na Ox a posunutý o 2 3 pozdĺž Ox doprava, hore o 2 jednotky pozdĺž Oy. Na súradnicovej čiare to vyzerá takto:

Yandex.RTB R-A-339285-1

Geometrické transformácie grafu funkcie

Aplikovaním geometrických transformácií daného grafu zistíme, že graf je znázornený funkciou tvaru ± k 1 · f (± k 2 · (x + a)) + b, keď k 1 > 0, k 2 > 0 sú kompresné koeficienty 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k2 > 1 pozdĺž Oy a Ox. Znamienko pred koeficientmi k 1 a k 2 označuje symetrické zobrazenie grafu vzhľadom na osi, a a b ho posúvajú pozdĺž O x a pozdĺž O y.

Definícia 1

Sú 3 typy geometrické transformácie grafu:

• Škálovanie pozdĺž O x a O y. Toto je ovplyvnené koeficientmi k 1 a k 2 za predpokladu, že sa nerovnajú 1, keď je 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, potom sa graf natiahne pozdĺž O y a stlačí pozdĺž O x.
• Symetrické zobrazenie vzhľadom na súradnicové osi. Ak je pred k 1 znamienko „-“, symetria je relatívna k O x a pred k 2 je relatívna k O y. Ak „-“ chýba, potom sa položka pri riešení preskočí;
• Paralelný prenos (zmena) pozdĺž O x a O y. Transformácia sa vykoná, ak sú koeficienty a a b rovné 0. Ak je a kladné, graf sa posunie doľava o | a | jednotiek, ak a je záporné, potom doprava v rovnakej vzdialenosti. Hodnota b určuje pohyb pozdĺž osi O y, čo znamená, že keď je b kladné, funkcia sa pohybuje nahor a ak je b záporná, pohybuje sa nadol.

Pozrime sa na riešenia pomocou príkladov, počnúc mocninou.

Príklad 1

Transformujte y = x 2 3 a nakreslite funkciu y = - 1 2 · 8 x - 4 2 3 + 3 .

Riešenie

Predstavme si funkcie takto:

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

Kde k 1 = 2, stojí za to venovať pozornosť prítomnosti „-“, a = - 1 2, b = 3. Odtiaľto dostávame, že geometrické transformácie sa vykonávajú natiahnutím pozdĺž O y dvakrát, zobrazené symetricky vzhľadom na O x, posunuté doprava o 1 2 a nahor o 3 jednotky.

Ak znázorníme pôvodnú mocenskú funkciu, dostaneme to

pri natiahnutí dvakrát pozdĺž O y máme to

Zobrazenie, symetrické vzhľadom na O x, má tvar

a posuňte sa doprava o 12

pohyb o 3 jednotky nahor vyzerá

Pozrime sa na transformácie exponenciálnych funkcií pomocou príkladov.

Príklad 2

Zostrojte graf exponenciálnej funkcie y = - 1 2 1 2 (2 - x) + 8.

Riešenie.

Transformujme funkciu na základe vlastností mocninovej funkcie. Potom to dostaneme

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

Z toho vidíme, že dostaneme reťaz transformácií y = 1 2 x:

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

Zistili sme, že pôvodná exponenciálna funkcia má tvar

Stlačenie na polovicu pozdĺž O y dáva

Natiahnutie pozdĺž O x

Symetrické zobrazenie vzhľadom na O x

Zobrazenie je symetrické vzhľadom na O y

Posuňte sa o 8 jednotiek vyššie

Uvažujme riešenie na príklade logaritmickej funkcie y = ln (x).

Príklad 3

Zostrojte funkciu y = ln e 2 · - 1 2 x 3 pomocou transformácie y = ln (x) .

Riešenie

Na vyriešenie je potrebné použiť vlastnosti logaritmu, potom dostaneme:

y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

Transformácia logaritmickej funkcie vyzerá takto:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

Nakreslíme pôvodnú logaritmickú funkciu

Stláčame sústavu podľa O y

Natiahneme sa pozdĺž O x

Vykonávame mapovanie vzhľadom na O y

Posunieme sa o 2 jednotky, dostaneme

Na transformáciu grafov goniometrickej funkcie je potrebné prispôsobiť schému riešenia v tvare ± k 1 · f (± k 2 · (x + a)) + b. Je potrebné, aby k2 bolo rovné Tk2. Odtiaľ dostaneme 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

Pozrime sa na príklady riešenia úloh s transformáciami y = sin x.

Príklad 4

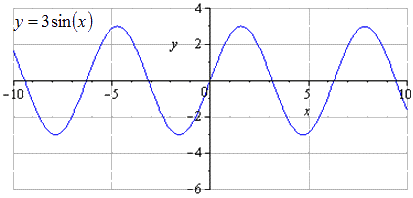
Zostrojte graf y = - 3 sin 1 2 x - 3 2 - 2 pomocou transformácií funkcie y=sinx.

Riešenie

Funkciu je potrebné zredukovať na tvar ± k 1 · f ± k 2 · x + a + b. Postup:

y = - 3 hriechy 1 2 x - 3 2 - 2 = - 3 hriechy 1 2 (x - 3) - 2

Je zrejmé, že k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Pretože pred k 1 je „-“, ale nie pred k 2, dostaneme reťaz transformácií tvaru:

y = hriech (x) → y = 3 hriech (x) → y = 3 hriech 1 2 x → y = - 3 hriech 1 2 x → → y = - 3 hriech 1 2 x - 3 → y = - 3 hriech 1 2 (x - 3) - 2

Detailná sínusová transformácia. Pri vynesení pôvodnej sínusoidy y = sin (x) zistíme, že za najmenšiu kladnú periódu sa považuje T = 2 π. Nájdenie maxima v bodoch π 2 + 2 π · k; 1, a minimum - - π 2 + 2 π · k; - 1, k ∈ Z.

O y sa natiahne trojnásobne, čo znamená, že zvýšenie amplitúdy kmitov sa zvýši 3-krát. T = 2 π je najmenšia kladná perióda. Maximá idú do π 2 + 2 π · k; 3, k ∈ Z, minimá - - π 2 + 2 π · k; - 3, k ∈ Z.

Pri natiahnutí pozdĺž O x na polovicu zistíme, že najmenšia kladná perióda sa zväčší 2-krát a rovná sa T = 2 π k 2 = 4 π. Maximá idú do π + 4 π · k; 3, k ∈ Z, minimá – v - π + 4 π · k; - 3, k ∈ Z.

Obraz je vytvorený symetricky vzhľadom na Ox. Najmenšie pozitívne obdobie v v tomto prípade sa nemení a rovná sa T = 2 π k 2 = 4 π . Maximálny prechod vyzerá takto - π + 4 π · k; 3, k ∈ Z a minimum je π + 4 π · k; - 3, k ∈ Z.

Graf je posunutý nadol o 2 jednotky. Minimálna spoločná doba sa nemení. Nálezové maximá s prechodom do bodov - π + 3 + 4 π · k; 1, k ∈ Z, minimá - π + 3 + 4 π · k; - 5, k∈Z.

V tomto štádiu sa graf goniometrickej funkcie považuje za transformovaný.

Uvažujme podrobnú transformáciu funkcie y = cos x.

Príklad 5

Zostrojte graf funkcie y = 3 2 cos 2 - 2 x + 1 pomocou transformácie funkcie v tvare y = cos x.

Riešenie

Podľa algoritmu je potrebné danú funkciu zredukovať na tvar ± k 1 · f ± k 2 · x + a + b. Potom to dostaneme

y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1

Z podmienky je zrejmé, že k 1 = 3 2, k 2 = 2, a = - 1, b = 1, kde k 2 má „-“, ale pred k 1 chýba.

Z toho vidíme, že dostaneme graf goniometrickej funkcie tvaru:

y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1 )) → y = 3 2 cos - 2 (x - 1) + 1

Krok za krokom kosínusová transformácia s grafickým znázornením.

Vzhľadom na graf y = cos(x) je zrejmé, že najkratšia celková perióda je T = 2π. Nájdenie maxima v 2 π · k ; 1, k ∈ Z a sú π + 2 π · k minimá; - 1, k ∈ Z.

Pri natiahnutí pozdĺž Oy 3 2 krát sa amplitúda kmitov zvýši 3 2 krát. T = 2 π je najmenšia kladná perióda. Nájdenie maxima v 2 π · k ; 3 2, k ∈ Z, minimá v π + 2 π · k; - 3 2, k ∈ Z .

Pri stlačení pozdĺž O x na polovicu zistíme, že najmenšia kladná perióda je číslo T = 2 π k 2 = π. Nastáva prechod maxím do π · k; 3 2 , k ∈ Z , minimá - π 2 + π · k ; - 3 2, k ∈ Z .

Symetrické mapovanie vzhľadom na Oy. Keďže je graf nepárny, nezmení sa.

Keď sa graf posunie o 1. V najmenšej kladnej perióde T = π nie sú žiadne zmeny. Hľadanie maxím v π · k + 1 ; 3 2, k ∈ Z, minimá - π 2 + 1 + π · k; - 3 2, k ∈ Z .

Pri posunutí o 1 sa najmenšia kladná perióda rovná T = π a nemení sa. Hľadanie maxím v π · k + 1 ; 5 2, k ∈ Z, minimá v π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Transformácia kosínusovej funkcie je dokončená.

Uvažujme transformácie pomocou príkladu y = t g x.

Príklad 6

Zostrojte graf funkcie y = - 1 2 t g π 3 - 2 3 x + π 3 pomocou transformácií funkcie y = t g (x) .

Riešenie

Na začiatok je potrebné zredukovať danú funkciu na tvar ± k 1 · f ± k 2 · x + a + b, po čom dostaneme, že

y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3

Je jasne viditeľné, že k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3 a pred koeficientmi k 1 a k 2 je „-“. To znamená, že po transformácii dostaneme tangensoidy

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3

Postupná transformácia dotyčníc s grafickým znázornením.

Máme, že pôvodný graf je y = t g (x) . Zmena kladnej periódy sa rovná T = π. Za oblasť definície sa považuje - π 2 + π · k ; π 2 + π · k, k ∈ Z.

2x stlačíme pozdĺž Oy. T = π sa považuje za najmenšiu kladnú periódu, kde doména definície má tvar - π 2 + π · k; π 2 + π · k, k ∈ Z.

Natiahnite sa pozdĺž O x 3 2-krát. Vypočítajme najmenšiu kladnú periódu a rovnala sa T = π k 2 = 3 2 π . A definičný obor funkcie so súradnicami je 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, mení sa len definičný obor.

Symetria ide na strane O x. Obdobie sa v tomto bode nezmení.

Súradnicové osi je potrebné zobraziť symetricky. Oblasť definície je v tomto prípade nezmenená. Harmonogram sa zhoduje s predchádzajúcim. To naznačuje, že funkcia dotyčnice je nepárna. Ak nepárnej funkcii priradíme symetrické zobrazenie O x a O y, tak ju transformujeme na pôvodnú funkciu.

Text práce je uverejnený bez obrázkov a vzorcov.
Plná verzia diela je dostupná v záložke „Pracovné súbory“ vo formáte PDF

Úvod

Transformácia funkčných grafov je jedným zo základných matematických pojmov priamo súvisiacich s praktickou činnosťou. S transformáciou grafov funkcií sa prvýkrát stretneme v algebre 9. ročníka pri štúdiu témy „Kvadratická funkcia“. Kvadratická funkcia je predstavená a študovaná v úzkej súvislosti s kvadratickými rovnicami a nerovnicami. Mnohé matematické pojmy sa tiež zvažujú grafickými metódami, napríklad v ročníkoch 10-11 štúdium funkcie umožňuje nájsť definičný obor a definičný obor funkcie, klesajúce alebo rastúce obory, asymptoty. , intervaly konštantného znamienka atď. Táto dôležitá otázka je tiež predmetom GIA. Z toho vyplýva, že konštruovanie a transformácia funkčných grafov je jednou z hlavných úloh vyučovania matematiky v škole.

Na vykreslenie grafov mnohých funkcií však môžete použiť množstvo metód, ktoré uľahčujú vykresľovanie. Vyššie uvedené určuje relevantnosť výskumné témy.

Predmet štúdia je študovať transformáciu grafov v školskej matematike.

Predmet výskumu - proces konštrukcie a transformácie funkčných grafov na strednej škole.

Problematická otázka: Je možné zostrojiť graf neznámej funkcie, ak máte zručnosť konvertovať grafy elementárnych funkcií?

Cieľ: vykresľovanie funkcií v neznámej situácii.

Úlohy:

1. Analyzujte vzdelávací materiál o skúmanom probléme. 2. Identifikujte schémy na transformáciu funkčných grafov v školskom kurze matematiky. 3. Vyberte najefektívnejšie metódy a prostriedky na vytváranie a transformáciu grafov funkcií. 4. Vedieť aplikovať túto teóriu pri riešení problémov.

Požadované počiatočné znalosti, zručnosti a schopnosti:

Určte hodnotu funkcie hodnotou argumentu rôznymi spôsobmi špecifikácie funkcie;

Vytvorte grafy študovaných funkcií;

Opíšte správanie a vlastnosti funkcií pomocou grafu a v najjednoduchších prípadoch pomocou vzorca nájdite najväčšie a najmenšie hodnoty z grafu funkcie;

Popisy pomocou funkcií rôznych závislostí, ich grafické znázornenie, interpretácia grafov.

Hlavná časť

Teoretická časť

Ako počiatočný graf funkcie y = f(x) zvolím kvadratickú funkciu y = x 2 . Zvážim prípady transformácie tohto grafu spojené so zmenami vo vzorci, ktorý definuje túto funkciu a vyvodím závery pre akúkoľvek funkciu.

1. Funkcia y = f(x) + a

V novom vzorci sa funkčné hodnoty (súradnice bodov grafu) menia o číslo a v porovnaní so „starou“ funkčnou hodnotou. To vedie k paralelnému prenosu funkčného grafu pozdĺž osi OY:

hore, ak a > 0; dole ak a< 0.

ZÁVER

Graf funkcie y=f(x)+a sa teda získa z grafu funkcie y=f(x) pomocou paralelného posunu pozdĺž osi y o jednotky nahor, ak a > 0, a o jednotky nadol. ak a< 0.

2. Funkcia y = f(x-a),

V novom vzorci sa hodnoty argumentov (úsečky bodov grafu) menia o číslo a v porovnaní so „starou“ hodnotou argumentu. To vedie k paralelnému prenosu funkčného grafu pozdĺž osi OX: doprava, ak a< 0, влево, если a >0.

ZÁVER

To znamená, že graf funkcie y= f(x - a) získame z grafu funkcie y=f(x) paralelným posunom pozdĺž osi x o jednotky doľava, ak a > 0, a jednotky vpravo, ak a< 0.

3. Funkcia y = k f(x), kde k > 0 a k ≠ 1

V novom vzorci sa funkčné hodnoty (súradnice bodov grafu) menia k-krát v porovnaní so „starou“ funkčnou hodnotou. To vedie k: 1) „natiahnutiu“ z bodu (0; 0) pozdĺž osi OY faktorom k, ak k > 1, 2) „stlačeniu“ do bodu (0; 0) pozdĺž osi OY o faktor, ak je 0< k < 1.

ZÁVER

Následne: na zostrojenie grafu funkcie y = kf(x), kde k > 0 ak ≠ 1, je potrebné vynásobiť ordináty bodov daného grafu funkcie y = f(x) číslom k. Takáto transformácia sa nazýva preťahovanie z bodu (0; 0) pozdĺž osi OY k krát, ak k > 1; kompresia do bodu (0; 0) pozdĺž osi OY krát, ak je 0< k < 1.

4. Funkcia y = f(kx), kde k > 0 a k ≠ 1

V novom vzorci sa hodnoty argumentov (úsečky bodov grafu) menia k-krát v porovnaní so „starou“ hodnotou argumentu. To vedie k: 1) „natiahnutiu“ z bodu (0; 0) pozdĺž osi OX 1/k krát, ak je 0< k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

ZÁVER

A tak: na zostavenie grafu funkcie y = f(kx), kde k > 0 a k ≠ 1, je potrebné vynásobiť úsečku bodov daného grafu funkcie y=f(x) číslom k . Takáto transformácia sa nazýva natiahnutie z bodu (0; 0) pozdĺž osi OX 1/k krát, ak je 0< k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

5. Funkcia y = - f (x).

V tomto vzorci sú hodnoty funkcií (súradnice bodov grafu) obrátené. Táto zmena vedie k symetrickému zobrazeniu pôvodného grafu funkcie vzhľadom na os Ox.

ZÁVER

Na vykreslenie grafu funkcie y = - f (x) potrebujete graf funkcie y= f(x)

odrážať symetricky okolo osi OX. Táto transformácia sa nazýva symetrická transformácia okolo osi OX.

6. Funkcia y = f (-x).

V tomto vzorci sú hodnoty argumentu (abscisa bodov grafu) obrátené. Táto zmena vedie k symetrickému zobrazeniu pôvodného grafu funkcie vzhľadom na os OY.

Príklad pre funkciu y = - x² táto transformácia nie je viditeľná, pretože táto funkcia je párna a graf sa po transformácii nemení. Táto transformácia je viditeľná, keď je funkcia nepárna a keď nie je ani párna, ani nepárna.

7. Funkcia y = |f(x)|.

V novom vzorci sú hodnoty funkcií (súradnice bodov grafu) pod znamienkom modulu. To vedie k vymiznutiu častí grafu pôvodnej funkcie so zápornými ordinátami (t. j. tých, ktoré sa nachádzajú v dolnej polrovine vzhľadom na os Ox) a k symetrickému zobrazeniu týchto častí vzhľadom k osi Ox.

8. Funkcia y= f (|x|).

V novom vzorci sú hodnoty argumentov (úsečky bodov grafu) pod znamienkom modulu. To vedie k vymiznutiu častí grafu pôvodnej funkcie so zápornými úsečkami (t. j. umiestnených v ľavej polrovine vzhľadom na os OY) a ich nahradeniu časťami pôvodného grafu, ktoré sú symetrické vzhľadom na os OY. .

Praktická časť

Pozrime sa na niekoľko príkladov aplikácie vyššie uvedenej teórie.

PRÍKLAD 1.

Riešenie. Transformujme tento vzorec:

1) Zostavme graf funkcie

PRÍKLAD 2.

Nakreslite graf funkcie danej vzorcom

Riešenie. Transformujme tento vzorec izoláciou druhej mocniny binomu v tomto kvadratickom trinome:

1) Zostavme graf funkcie

2) Vykonajte paralelný prenos zostrojeného grafu do vektora

PRÍKLAD 3.

ÚLOHA Z Jednotnej štátnej skúšky Vytvorenie grafu funkcie po častiach

Graf funkcie Graf funkcie y=|2(x-3)2-2|; 1

V závislosti od podmienok fyzikálnych procesov niektoré veličiny nadobúdajú konštantné hodnoty a nazývajú sa konštanty, iné sa za určitých podmienok menia a nazývajú sa premenné.

Starostlivé štúdium prostredia ukazuje, že fyzikálne veličiny sú na sebe závislé, to znamená, že zmena niektorých veličín so sebou nesie aj zmenu iných.

Matematická analýza sa zaoberá štúdiom kvantitatívnych vzťahov medzi vzájomne sa meniacimi veličinami, pričom abstrahuje od špecifického fyzikálneho významu. Jedným zo základných pojmov matematickej analýzy je pojem funkcie.

Zvážte prvky súpravy a prvky súpravy
(obr. 3.1).

Ak sa medzi prvkami súborov vytvorí určitá korešpondencia
A vo forme pravidla , potom si všimnú, že funkcia je definovaná
.

Definícia 3.1. Korešpondencia , ktorý sa spája s každým prvkom nie prázdna množina
nejaký dobre definovaný prvok nie prázdna množina ,nazývaná funkcia alebo mapovanie
V .

Symbolicky zobraziť
V sa píše takto:

.

Zároveň mnohí
sa nazýva definičný obor funkcie a označuje sa
.

Na druhej strane mnohí sa nazýva rozsah hodnôt funkcie a označuje sa
.

Okrem toho je potrebné poznamenať, že prvky súpravy
sa nazývajú nezávislé premenné, prvky množiny sa nazývajú závislé premenné.

Metódy určenia funkcie

Funkciu je možné špecifikovať týmito hlavnými spôsobmi: tabuľkovo, graficky, analyticky.

Ak sa na základe experimentálnych údajov zostavia tabuľky, ktoré obsahujú hodnoty funkcie a zodpovedajúce hodnoty argumentov, potom sa táto metóda špecifikácie funkcie nazýva tabuľková.

Súčasne, ak sú niektoré štúdie experimentálneho výsledku zobrazené na rekordéri (osciloskop, rekordér atď.), Potom je potrebné poznamenať, že funkcia je špecifikovaná graficky.

Najbežnejší je analytický spôsob špecifikácie funkcie, t.j. metóda, v ktorej je nezávislá a závislá premenná spojená pomocou vzorca. V tomto prípade hrá významnú úlohu doména definície funkcie:

rozdielne, hoci sú dané rovnakými analytickými vzťahmi.

Ak zadáte iba vzorec funkcie
, potom uvažujeme, že oblasť definície tejto funkcie sa zhoduje s množinou týchto hodnôt premennej , pre ktorý výraz
dáva zmysel. V tomto smere zohráva osobitnú úlohu problém hľadania definičného oboru funkcie.

Úloha 3.1. Nájdite doménu funkcie

Riešenie

Prvý termín nadobúda skutočné hodnoty, keď
, a druhý o. Na nájdenie oblasti definície danej funkcie je teda potrebné vyriešiť systém nerovností:

Výsledkom je riešenie takéhoto systému. Preto doménou definície funkcie je segment
.

Najjednoduchšie transformácie funkčných grafov

Konštrukciu grafov funkcií je možné výrazne zjednodušiť, ak použijete známe grafy základných elementárnych funkcií. Nasledujúce funkcie sa nazývajú hlavné elementárne funkcie:

1) funkcia napájania
Kde
;

2) exponenciálna funkcia
Kde
A
;

3) logaritmická funkcia
, Kde - akékoľvek kladné číslo iné ako jedna:
A
;

4) goniometrické funkcie




;
.

5) inverzné goniometrické funkcie
;
;
;
.

Elementárne funkcie sú funkcie, ktoré sa získavajú zo základných elementárnych funkcií pomocou štyroch aritmetických operácií a superpozícií aplikovaných v konečnom počte krát.

Jednoduché geometrické transformácie tiež umožňujú zjednodušiť proces konštrukcie grafu funkcií. Tieto transformácie sú založené na nasledujúcich tvrdeniach:

Graf funkcie y=f(x+a) je graf y=f(x), posunutý (pre a >0 doľava, pre a< 0 вправо) на |a| единиц параллельно осиOx.

Graf funkcie y=f(x) +b je graf y=f(x), posunutý (pri b>0 hore, pri b< 0 вниз) на |b| единиц параллельно осиOy.

Graf funkcie y = mf(x) (m0) je graf y = f(x), natiahnutý (pri m>1) m-krát alebo stlačený (pri 0

Graf funkcie y = f(kx) je graf y = f(x), stlačený (pre k >1) k-krát alebo natiahnutý (pre 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.

Hypotéza: Ak študujete pohyb grafu pri tvorbe rovnice funkcií, všimnete si, že všetky grafy sa riadia všeobecnými zákonmi, takže je možné formulovať všeobecné zákony bez ohľadu na funkcie, čo uľahčí nielen konštrukciu grafy rôznych funkcií, ale využiť ich aj pri riešení úloh.

Cieľ: Študovať pohyb grafov funkcií:

1) Úlohou je naštudovať literatúru

2) Naučte sa vytvárať grafy rôznych funkcií

3) Naučte sa transformovať grafy lineárnych funkcií

4) Zvážte problematiku používania grafov pri riešení úloh

Predmet štúdia: Funkčné grafy

Predmet výskumu: Pohyby funkčných grafov

Relevantnosť: Vytváranie grafov funkcií spravidla trvá veľa času a vyžaduje pozornosť zo strany študenta, ale so znalosťou pravidiel na prevod grafov funkcií a grafov základných funkcií môžete rýchlo a ľahko zostaviť grafy funkcií. , ktorý vám umožní nielen dokončiť úlohy týkajúce sa konštrukcie grafov funkcií, ale aj vyriešiť problémy s tým súvisiace (nájsť maximum (minimálna výška času a bod stretnutia))

Tento projekt je užitočný pre všetkých študentov školy.

Prehľad literatúry:

V literatúre sú rozoberané metódy na vytváranie grafov rôznych funkcií, ako aj príklady transformácie grafov týchto funkcií. Grafy takmer všetkých hlavných funkcií sa používajú v rôznych technických procesoch, čo vám umožňuje jasnejšie vizualizovať tok procesu a naprogramovať výsledok

Trvalá funkcia. Táto funkcia je daná vzorcom y = b, kde b je určité číslo. Graf konštantnej funkcie je priamka rovnobežná s úsečkou a prechádzajúca bodom (0; b) na zvislej osi. Graf funkcie y = 0 je os x.

Typy funkcií 1Priama úmernosť. Táto funkcia je daná vzorcom y = kx, kde koeficient úmernosti k ≠ 0. Grafom priamej úmernosti je priamka prechádzajúca počiatkom.

Lineárna funkcia. Takáto funkcia je daná vzorcom y = kx + b, kde k a b sú reálne čísla. Graf lineárnej funkcie je priamka.

Grafy lineárnych funkcií sa môžu pretínať alebo byť rovnobežné.

Čiary grafov lineárnych funkcií y = k 1 x + b 1 a y = k 2 x + b 2 sa teda pretínajú, ak k 1 ≠ k 2 ; ak k 1 = k 2, potom sú čiary rovnobežné.

2Inverzná úmernosť je funkcia, ktorá je daná vzorcom y = k/x, kde k ≠ 0. K sa nazýva koeficient nepriamej úmernosti. Grafom nepriamej úmernosti je hyperbola.

Funkciu y = x 2 predstavuje graf nazývaný parabola: na intervale [-~; 0] funkcia klesá, v intervale sa funkcia zvyšuje.

Funkcia y = x 3 narastá pozdĺž celej číselnej osi a je graficky znázornená kubickou parabolou.

Mocninná funkcia s prirodzeným exponentom. Táto funkcia je daná vzorcom y = x n, kde n je prirodzené číslo. Grafy mocninnej funkcie s prirodzeným exponentom závisia od n. Napríklad, ak n = 1, potom graf bude priamka (y = x), ak n = 2, potom bude graf parabola atď.

Mocninná funkcia so záporným celočíselným exponentom je vyjadrená vzorcom y = x -n, kde n je prirodzené číslo. Táto funkcia je definovaná pre všetky x ≠ 0. Graf funkcie závisí aj od exponentu n.

Mocninná funkcia s kladným zlomkovým exponentom. Táto funkcia je vyjadrená vzorcom y = x r, kde r je kladný neredukovateľný zlomok. Táto funkcia tiež nie je párna ani nepárna.

Čiarový graf, ktorý zobrazuje vzťah medzi závislými a nezávislými premennými na rovine súradníc. Graf slúži na vizuálne zobrazenie týchto prvkov

Nezávislá premenná je premenná, ktorá môže nadobúdať akúkoľvek hodnotu v oblasti definície funkcie (kde má táto funkcia význam (nedá sa deliť nulou))

Na vytvorenie grafu funkcií, ktoré potrebujete

1) Nájdite VA (rozsah prijateľných hodnôt)

2) vziať niekoľko ľubovoľných hodnôt pre nezávislú premennú

3) Nájdite hodnotu závislej premennej

4) Zostrojte súradnicovú rovinu a vyznačte na nej tieto body

5) Spojte ich čiary, ak je to potrebné, preskúmajte výsledný graf Transformácia grafov elementárnych funkcií.

Prevod grafov

V čistej forme nie sú základné elementárne funkcie, žiaľ, také bežné. Oveľa častejšie sa musíte zaoberať elementárnymi funkciami získanými zo základných elementárnych sčítaním konštánt a koeficientov. Grafy takýchto funkcií je možné zostrojiť aplikáciou geometrických transformácií na grafy príslušných základných elementárnych funkcií (alebo prepnutím na nový súradnicový systém). Napríklad vzorec kvadratickej funkcie je vzorec kvadratickej paraboly, trikrát stlačený vzhľadom na zvislú os, symetricky zobrazený vzhľadom na os x, posunutý proti smeru tejto osi o 2/3 jednotiek a posunutý pozdĺž osi y o 2 jednotiek.

Pochopme tieto geometrické transformácie grafu funkcie krok za krokom na konkrétnych príkladoch.

Pomocou geometrických transformácií grafu funkcie f(x) možno zostaviť graf ľubovoľnej funkcie formulárového vzorca, kde vzorec sú koeficienty kompresie alebo roztiahnutia pozdĺž osi oy a ox, znamienka mínus vpredu. Koeficienty vzorca a vzorca označujú symetrické zobrazenie grafu vzhľadom na súradnicové osi , a a b určujú posun vzhľadom na súradnicovú a ordinátnu os.

Existujú teda tri typy geometrických transformácií grafu funkcie:

Prvým typom je škálovanie (stlačenie alebo natiahnutie) pozdĺž osi x a zvislej osi.

Potreba škálovania je indikovaná inými koeficientmi vzorca ako jedna, ak je číslo menšie ako 1, potom sa graf stlačí vzhľadom na oy a natiahne sa vzhľadom na ox, ak je číslo väčšie ako 1, potom sa natiahneme pozdĺž osi y; a stlačte pozdĺž osi x.

Druhým typom je symetrické (zrkadlové) zobrazenie vzhľadom na súradnicové osi.

Potrebu tejto transformácie naznačujú znamienko mínus pred koeficientmi vzorca (v tomto prípade zobrazujeme graf symetricky podľa osi ox) a vzorca (v tomto prípade zobrazujeme graf symetricky podľa oy os). Ak neexistujú žiadne znamienka mínus, tento krok sa preskočí.