การเคลื่อนที่ของกราฟฟังก์ชัน การแปลงกราฟฟังก์ชัน

กลับไปข้างหน้า

ความสนใจ! การแสดงตัวอย่างสไลด์มีวัตถุประสงค์เพื่อให้ข้อมูลเท่านั้น และอาจไม่ได้แสดงถึงคุณลักษณะทั้งหมดของงานนำเสนอ หากสนใจงานนี้กรุณาดาวน์โหลดฉบับเต็ม

วัตถุประสงค์ของบทเรียน:กำหนดรูปแบบของการแปลงกราฟฟังก์ชัน

งาน:

ทางการศึกษา:

• สอนนักเรียนให้สร้างกราฟของฟังก์ชันโดยการแปลงกราฟของฟังก์ชันที่กำหนด โดยใช้การแปลแบบขนาน การบีบอัด (การยืด) และสมมาตรประเภทต่างๆ

ทางการศึกษา:

• เพื่อปลูกฝังคุณสมบัติส่วนบุคคลของผู้เรียน (ความสามารถในการฟัง) ความปรารถนาดีต่อผู้อื่น ความเอาใจใส่ ความถูกต้อง มีระเบียบวินัย และความสามารถในการทำงานเป็นกลุ่ม
• ปลูกฝังความสนใจในเรื่องและความจำเป็นในการได้รับความรู้

พัฒนาการ:

• เพื่อพัฒนาจินตนาการเชิงพื้นที่และการคิดเชิงตรรกะของนักเรียน ความสามารถในการสำรวจสภาพแวดล้อมได้อย่างรวดเร็ว พัฒนาสติปัญญา ไหวพริบ และฝึกความจำ

อุปกรณ์:

• การติดตั้งมัลติมีเดีย: คอมพิวเตอร์, โปรเจ็กเตอร์

วรรณกรรม:

1. Bashmakov, M. I. คณิตศาสตร์ [ข้อความ]: หนังสือเรียนสำหรับสถาบันเริ่มต้น และวันพุธ ศาสตราจารย์ การศึกษา / M.I. Bashmakov - ฉบับที่ 5 แก้ไขแล้ว – อ.: ศูนย์สำนักพิมพ์ “Academy”, 2555. – 256 น.
2. Bashmakov, M. I. คณิตศาสตร์ หนังสือปัญหา [ข้อความ]: หนังสือเรียน

ค่าเผื่อการศึกษา สถาบันตั้งแต่เนิ่นๆ และวันพุธ

1. ศาสตราจารย์ การศึกษา / M. I. Bashmakov – M.: Publishing Center “Academy”, 2012. – 416 p.
2. แผนการสอน:
3. ช่วงเวลาขององค์กร (3 นาที)
4. การอัพเดตความรู้ (7 นาที)
5. คำอธิบายเนื้อหาใหม่ (20 นาที)
6. การรวมวัสดุใหม่ (10 นาที)

สรุปบทเรียน (3 นาที)

การบ้าน (2 นาที)

ความคืบหน้าของบทเรียน

1. องค์กร ช่วงเวลา (3 นาที)

กำลังตรวจสอบสิ่งที่มีอยู่

สื่อสารจุดประสงค์ของบทเรียน

ก่อนที่เราจะพูดถึงการแปลงกราฟ เรามาทบทวนเนื้อหาที่เรากล่าวถึงกันก่อน

งานช่องปาก. (สไลด์ 2)

ฟังก์ชั่นที่กำหนด:

3. อธิบายกราฟของฟังก์ชัน: , , , .

3. คำอธิบายเนื้อหาใหม่ (20 นาที)

การแปลงกราฟที่ง่ายที่สุดคือการถ่ายโอนแบบขนาน การบีบอัด (การยืด) และสมมาตรบางประเภท การเปลี่ยนแปลงบางอย่างแสดงอยู่ในตาราง (ภาคผนวก 1), (สไลด์ 3)

ทำงานเป็นกลุ่ม.

แต่ละกลุ่มสร้างกราฟของฟังก์ชันที่กำหนดและนำเสนอผลการอภิปราย

การทำงาน	การแปลงกราฟของฟังก์ชัน	ตัวอย่างฟังก์ชัน	สไลด์
	โอ้บน กหน่วยขึ้นถ้า ก>0 และบน |A| หน่วยลงถ้า ก<0.	,	(สไลด์ 4)
	การถ่ายโอนแบบขนานไปตามแกน โอ้บน กหน่วยทางด้านขวาถ้า ก>0 และต่อไป - กหน่วยทางด้านซ้ายถ้า ก<0.	,	(สไลด์ 5)

ฟังก์ชันพื้นฐานพื้นฐานในรูปแบบบริสุทธิ์โดยไม่มีการแปลงนั้นหาได้ยาก ดังนั้นบ่อยครั้งที่คุณต้องทำงานกับฟังก์ชันพื้นฐานที่ได้รับจากฟังก์ชันหลักโดยการบวกค่าคงที่และสัมประสิทธิ์ กราฟดังกล่าวถูกสร้างขึ้นโดยใช้การแปลงทางเรขาคณิตของฟังก์ชันพื้นฐานที่กำหนด

ลองพิจารณาตัวอย่างฟังก์ชันกำลังสองในรูปแบบ y = - 1 3 x + 2 3 2 + 2 ซึ่งกราฟคือพาราโบลา y = x 2 ซึ่งถูกบีบอัดสามครั้งด้วยความเคารพต่อ Oy และสมมาตรด้วยความเคารพ ถึง Ox ​​และเลื่อนไป 2 3 ตาม Ox ไปทางขวา ขึ้น 2 หน่วยตาม Oy บนเส้นพิกัดจะมีลักษณะดังนี้:

ยานเดกซ์ RTB R-A-339285-1

การแปลงเรขาคณิตของกราฟของฟังก์ชัน

เมื่อใช้การแปลงทางเรขาคณิตของกราฟที่กำหนด เราพบว่ากราฟแสดงด้วยฟังก์ชันในรูปแบบ ± k 1 · f (± k 2 · (x + a)) + b เมื่อ k 1 > 0, k 2 > 0 คือค่าสัมประสิทธิ์การบีบอัดที่ 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 ตาม O y และ O x เครื่องหมายที่อยู่หน้าค่าสัมประสิทธิ์ k 1 และ k 2 บ่งบอกถึงการแสดงกราฟแบบสมมาตรสัมพันธ์กับแกน a และ b เลื่อนไปตาม O x และตาม O y

คำจำกัดความ 1

มี 3 ประเภท การแปลงทางเรขาคณิตของกราฟ:

• การปรับขนาดตาม O x และ O y สิ่งนี้ได้รับอิทธิพลจากสัมประสิทธิ์ k 1 และ k 2 โดยมีเงื่อนไขว่าไม่เท่ากับ 1 เมื่อ 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1 จากนั้นกราฟจะยืดไปตาม O y และบีบอัดไปตาม O x
• การแสดงผลแบบสมมาตรสัมพันธ์กับแกนพิกัดหากมีเครื่องหมาย “-” หน้า k 1 ความสมมาตรจะสัมพันธ์กับ O x และหน้า k 2 จะสัมพันธ์กับ O y หากไม่มี "-" แสดงว่ารายการนั้นถูกข้ามไปเมื่อทำการแก้ไข
• การถ่ายโอนแบบขนาน (กะ)ตาม O x และ O y การแปลงจะดำเนินการหากมีค่าสัมประสิทธิ์ a และ b ไม่เท่ากับ 0 หาก a เป็นบวก กราฟจะเลื่อนไปทางซ้ายด้วย | ก | หน่วย ถ้า a เป็นลบ ให้ไปทางขวาที่ระยะเท่ากัน ค่า b กำหนดการเคลื่อนที่ตามแนวแกน O y ซึ่งหมายความว่าเมื่อ b เป็นบวก ฟังก์ชันจะเลื่อนขึ้น และเมื่อ b เป็นลบ ฟังก์ชันจะเลื่อนลง

มาดูวิธีแก้ปัญหาโดยใช้ตัวอย่าง โดยเริ่มจากฟังก์ชันกำลัง

ตัวอย่างที่ 1

แปลง y = x 2 3 และพลอตฟังก์ชัน y = - 1 2 · 8 x - 4 2 3 + 3

สารละลาย

ลองจินตนาการถึงฟังก์ชันดังนี้:

y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3

โดยที่ k 1 = 2 ควรให้ความสนใจกับการมี "-", a = - 1 2, b = 3 จากจุดนี้ เราพบว่าการแปลงทางเรขาคณิตทำได้โดยการยืดไปตาม O y สองครั้ง โดยแสดงสัมพันธ์กับ O x แบบสมมาตร และเลื่อนไปทางขวา 1 2 และขึ้นไป 3 หน่วย

ถ้าเราพรรณนาถึงฟังก์ชันกำลังดั้งเดิม เราจะได้สิ่งนั้น

เมื่อยืดออกไปสองครั้ง โอ้ เราก็ได้อย่างนั้น

การแมปซึ่งสมมาตรด้วยความเคารพต่อ O x มีรูปแบบ

และเลื่อนไปทางขวา 1 2

การเคลื่อนไหว 3 หน่วยขึ้นไปดูเหมือน

ลองดูการแปลงฟังก์ชันเลขชี้กำลังโดยใช้ตัวอย่าง

ตัวอย่างที่ 2

สร้างกราฟของฟังก์ชันเลขชี้กำลัง y = - 1 2 1 2 (2 - x) + 8

สารละลาย.

เรามาแปลงฟังก์ชันตามคุณสมบัติของฟังก์ชันกำลังกันดีกว่า แล้วเราจะได้รับสิ่งนั้น

y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8

จากนี้เราจะเห็นว่าเราได้รับห่วงโซ่ของการแปลง y = 1 2 x:

y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8

เราพบว่าฟังก์ชันเลขชี้กำลังดั้งเดิมมีรูปแบบ

บีบสองครั้งตามโอ้ให้

ยืดเหยียดไปตาม O x

การทำแผนที่สมมาตรเทียบกับ O x

การทำแผนที่มีความสมมาตรด้วยความเคารพต่อ O y

ขยับขึ้น 8 หน่วย

ลองพิจารณาวิธีแก้ปัญหาโดยใช้ตัวอย่างฟังก์ชันลอการิทึม y = ln (x)

ตัวอย่างที่ 3

สร้างฟังก์ชัน y = ln e 2 · - 1 2 x 3 โดยใช้การแปลง y = ln (x)

สารละลาย

ในการแก้ปัญหา จำเป็นต้องใช้คุณสมบัติของลอการิทึม จากนั้นเราจะได้:

y = ln อี 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2

การแปลงฟังก์ชันลอการิทึมมีลักษณะดังนี้:

y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2

ลองพลอตฟังก์ชันลอการิทึมดั้งเดิมกัน

เราบีบอัดระบบตาม O y

เรายืดไปตาม O x

เราทำการแมปด้วยความเคารพต่อ O y

เราเลื่อนขึ้น 2 หน่วย เราได้

ในการแปลงกราฟของฟังก์ชันตรีโกณมิติ จำเป็นต้องปรับคำตอบของรูปแบบ ± k 1 · f (± k 2 · (x + a)) + b ให้เข้ากับโครงร่าง จำเป็นที่ k 2 จะเท่ากับ T k 2 . จากตรงนี้เราจะได้ 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.

ลองดูตัวอย่างการแก้ปัญหาเกี่ยวกับการแปลง y = sin x

ตัวอย่างที่ 4

สร้างกราฟของ y = - 3 sin 1 2 x - 3 2 - 2 โดยใช้การแปลงฟังก์ชัน y=sinx

สารละลาย

จำเป็นต้องลดฟังก์ชันให้อยู่ในรูปแบบ ± k 1 · f ± k 2 · x + a + b เมื่อต้องการทำสิ่งนี้:

y = - 3 บาป 1 2 x - 3 2 - 2 = - 3 บาป 1 2 (x - 3) - 2

จะเห็นได้ว่า k 1 = 3, k 2 = 1 2, a = - 3, b = - 2 เนื่องจากมี "-" ก่อน k 1 แต่ไม่ใช่ก่อน k 2 เราจึงได้ห่วงโซ่ของการเปลี่ยนแปลงของรูปแบบ:

y = บาป (x) → y = 3 บาป (x) → y = 3 บาป 1 2 x → y = - 3 บาป 1 2 x → → y = - 3 บาป 1 2 x - 3 → y = - 3 บาป 1 2 (x - 3) - 2

การแปลงคลื่นไซน์โดยละเอียด เมื่อวาดจุดไซน์ซอยด์ดั้งเดิม y = sin (x) เราพบว่าคาบบวกที่น้อยที่สุดถือเป็น T = 2 π ค้นหาค่าสูงสุดที่จุด π 2 + 2 π · k; 1 และค่าต่ำสุด - - π 2 + 2 π · k; - 1, k ∈ Z

O y ถูกยืดออกสามเท่า ซึ่งหมายความว่าแอมพลิจูดของการแกว่งจะเพิ่มขึ้น 3 เท่า T = 2 π คือคาบบวกที่น้อยที่สุด ค่าสูงสุดไปที่ π 2 + 2 π · k; 3, k ∈ Z, ขั้นต่ำ - - π 2 + 2 π · k; - 3, เค ∈ ซี

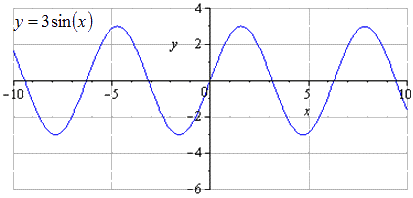
เมื่อยืดไปตาม O x ครึ่งหนึ่ง เราจะพบว่าคาบบวกที่น้อยที่สุดเพิ่มขึ้น 2 เท่า และเท่ากับ T = 2 π k 2 = 4 π ค่าสูงสุดไปที่ π + 4 π · k; 3, k ∈ Z, ค่าต่ำสุด – ใน - π + 4 π · k; - 3, เค ∈ ซี

ภาพถูกสร้างขึ้นอย่างสมมาตรด้วยความเคารพต่อ O x ช่วงบวกที่น้อยที่สุดใน ในกรณีนี้ไม่เปลี่ยนแปลงและเท่ากับ T = 2 π k 2 = 4 π . การเปลี่ยนแปลงสูงสุดดูเหมือน - π + 4 π · k; 3, k ∈ Z และค่าต่ำสุดคือ π + 4 π · k; - 3, เค ∈ ซี

กราฟเลื่อนลง 2 หน่วย ไม่มีการเปลี่ยนแปลงระยะเวลาทั่วไปขั้นต่ำ การค้นหาสูงสุดด้วยการเปลี่ยนไปใช้จุด - π + 3 + 4 π · k; 1, k ∈ Z, ค่าต่ำสุด - π + 3 + 4 π · k; - 5 , k ∈ Z .

ในขั้นตอนนี้ กราฟของฟังก์ชันตรีโกณมิติจะถือว่าถูกแปลง

ลองพิจารณาการเปลี่ยนแปลงโดยละเอียดของฟังก์ชัน y = cos x

ตัวอย่างที่ 5

สร้างกราฟของฟังก์ชัน y = 3 2 cos 2 - 2 x + 1 โดยใช้การแปลงฟังก์ชันในรูปแบบ y = cos x

สารละลาย

ตามอัลกอริทึมจำเป็นต้องลดฟังก์ชันที่กำหนดให้อยู่ในรูปแบบ ± k 1 · f ± k 2 · x + a + b แล้วเราจะได้รับสิ่งนั้น

y = 3 2 คอส 2 - 2 x + 1 = 3 2 คอส (- 2 (x - 1)) + 1

จากเงื่อนไขเป็นที่ชัดเจนว่า k 1 = 3 2, k 2 = 2, a = - 1, b = 1 โดยที่ k 2 มี "-" และก่อน k 1 จะหายไป

จากนี้เราจะเห็นว่าเราได้กราฟของฟังก์ชันตรีโกณมิติของรูปแบบ:

y = คอส (x) → y = 3 2 คอส (x) → y = 3 2 คอส (2 x) → y = 3 2 คอส (- 2 x) → → y = 3 2 คอส (- 2 (x - 1 )) → y = 3 2 cos - 2 (x - 1) + 1

การแปลงโคไซน์ทีละขั้นตอนพร้อมภาพประกอบกราฟิก

เมื่อพิจารณาจากกราฟ y = cos(x) เห็นได้ชัดว่าคาบรวมที่สั้นที่สุดคือ T = 2π หาค่าสูงสุดใน 2 π · k ; 1, k ∈ Z และมี π + 2 π · k ขั้นต่ำ; - 1, k ∈ Z

เมื่อยืดไปตาม Oy 3 2 เท่า แอมพลิจูดของการแกว่งจะเพิ่มขึ้น 3 2 เท่า T = 2 π คือคาบบวกที่น้อยที่สุด หาค่าสูงสุดใน 2 π · k ; 3 2, k ∈ Z, ค่าต่ำสุดใน π + 2 π · k; - 3 2 , k ∈ Z .

เมื่อบีบอัดตาม O x ลงครึ่งหนึ่ง เราจะพบว่าคาบบวกที่น้อยที่สุดคือตัวเลข T = 2 π k 2 = π ค่าสูงสุดจะถูกโอนไปที่ π · k ; 3 2 , k ∈ Z , ค่าต่ำสุด - π 2 + π · k ; - 3 2 , k ∈ Z .

การทำแผนที่แบบสมมาตรเทียบกับ Oy เนื่องจากกราฟเป็นเลขคี่ มันจะไม่เปลี่ยนแปลง

เมื่อกราฟเลื่อนไป 1 ไม่มีการเปลี่ยนแปลงในช่วงเวลาบวกที่น้อยที่สุด T = π หาค่าสูงสุดใน π · k + 1 ; 3 2, k ∈ Z, ค่าต่ำสุด - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

เมื่อเลื่อนไป 1 คาบบวกที่น้อยที่สุดจะเท่ากับ T = π และไม่มีการเปลี่ยนแปลง หาค่าสูงสุดใน π · k + 1 ; 5 2, k ∈ Z, ขั้นต่ำใน π 2 + 1 + π · k; - 1 2 , k ∈ Z .

การแปลงฟังก์ชันโคไซน์เสร็จสมบูรณ์

ลองพิจารณาการแปลงโดยใช้ตัวอย่าง y = t g x

ตัวอย่างที่ 6

สร้างกราฟของฟังก์ชัน y = - 1 2 t g π 3 - 2 3 x + π 3 โดยใช้การแปลงฟังก์ชัน y = t g (x) .

สารละลาย

ขั้นแรกจำเป็นต้องลดฟังก์ชันที่กำหนดให้อยู่ในรูปแบบ ± k 1 · f ± k 2 · x + a + b หลังจากนั้นเราจะได้สิ่งนั้น

y = - 1 2 t ก. π 3 - 2 3 x + π 3 = - 1 2 t ก. - 2 3 x - π 2 + π 3

เห็นได้ชัดว่า k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3 และหน้าสัมประสิทธิ์ k 1 และ k 2 จะมี "-" ซึ่งหมายความว่าหลังจากเปลี่ยนแทนเจนต์แล้วเราจะได้

y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 ตัน ก. - 2 3 x - π 2 → → y = - 1 2 ตัน ก. - 2 3 x - π 2 + π 3

การแปลงแทนเจนต์ทีละขั้นตอนด้วยการแสดงกราฟิก

เรามีกราฟเดิมคือ y = t g (x) การเปลี่ยนแปลงในช่วงเวลาบวกจะเท่ากับ T = π โดเมนของคำจำกัดความถือเป็น - π 2 + π · k ; π 2 + π · k, k ∈ Z

เราบีบอัดมัน 2 ครั้งตามออย T = π ถือเป็นคาบบวกที่เล็กที่สุด โดยที่โดเมนของคำจำกัดความมีรูปแบบ - π 2 + π · k; π 2 + π · k, k ∈ Z

ยืดเหยียดตาม O x 3 2 ครั้ง ลองคำนวณคาบบวกที่น้อยที่สุด และจะเท่ากับ T = π k 2 = 3 2 π และโดเมนของคำจำกัดความของฟังก์ชันที่มีพิกัดคือ 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z เฉพาะโดเมนของคำจำกัดความเท่านั้นที่เปลี่ยนแปลง

สมมาตรไปทางด้าน O x ระยะเวลาจะไม่เปลี่ยนแปลง ณ จุดนี้

จำเป็นต้องแสดงแกนพิกัดแบบสมมาตร ขอบเขตของคำจำกัดความในกรณีนี้ไม่มีการเปลี่ยนแปลง กำหนดการตรงกับกำหนดการก่อนหน้า นี่แสดงว่าฟังก์ชันแทนเจนต์เป็นเลขคี่ หากเรากำหนดการแมปสมมาตรของ O x และ O y ให้กับฟังก์ชันคี่ เราจะแปลงมันเป็นฟังก์ชันดั้งเดิม

ข้อความของงานถูกโพสต์โดยไม่มีรูปภาพและสูตร
ผลงานเวอร์ชันเต็มมีอยู่ในแท็บ "ไฟล์งาน" ในรูปแบบ PDF

การแนะนำ

การแปลงกราฟฟังก์ชันเป็นหนึ่งในแนวคิดทางคณิตศาสตร์พื้นฐานที่เกี่ยวข้องโดยตรงกับกิจกรรมภาคปฏิบัติ การแปลงกราฟของฟังก์ชันพบครั้งแรกในพีชคณิตชั้นประถมศึกษาปีที่ 9 เมื่อศึกษาหัวข้อ "ฟังก์ชันกำลังสอง" ฟังก์ชันกำลังสองถูกนำมาใช้และศึกษาโดยเชื่อมโยงอย่างใกล้ชิดกับสมการกำลังสองและอสมการ นอกจากนี้ แนวคิดทางคณิตศาสตร์จำนวนมากยังได้รับการพิจารณาโดยวิธีกราฟิก เช่น ในเกรด 10-11 การศึกษาฟังก์ชันทำให้สามารถค้นหาโดเมนของคำจำกัดความและโดเมนของค่าของฟังก์ชัน โดเมนของการลดลงหรือเพิ่มขึ้น เส้นกำกับ , ช่วงเวลาของสัญญาณคงที่ ฯลฯ GIA ยังได้หยิบยกประเด็นสำคัญนี้ขึ้นมาด้วย ตามมาด้วยการสร้างและการแปลงกราฟฟังก์ชันเป็นหนึ่งในงานหลักในการสอนคณิตศาสตร์ที่โรงเรียน

อย่างไรก็ตาม ในการพล็อตกราฟของหลายฟังก์ชัน คุณสามารถใช้วิธีการต่างๆ มากมายที่ทำให้การพล็อตง่ายขึ้น ข้างต้นกำหนด ความเกี่ยวข้องหัวข้อการวิจัย

วัตถุประสงค์ของการศึกษาคือการศึกษาการเปลี่ยนแปลงของกราฟในวิชาคณิตศาสตร์ของโรงเรียน

หัวข้อการวิจัย -กระบวนการสร้างและแปลงฟังก์ชันกราฟในโรงเรียนมัธยมศึกษา

คำถามที่มีปัญหา: เป็นไปได้ไหมที่จะสร้างกราฟของฟังก์ชันที่ไม่คุ้นเคยหากคุณมีทักษะในการแปลงกราฟของฟังก์ชันพื้นฐาน

เป้า:การวางแผนฟังก์ชันในสถานการณ์ที่ไม่คุ้นเคย

งาน:

1. วิเคราะห์สื่อการศึกษาเกี่ยวกับปัญหาที่กำลังศึกษา 2. ระบุแผนการสำหรับการแปลงกราฟฟังก์ชันในหลักสูตรคณิตศาสตร์ของโรงเรียน 3. เลือกวิธีการและวิธีการที่มีประสิทธิภาพสูงสุดในการสร้างและแปลงกราฟฟังก์ชัน 4.สามารถนำทฤษฎีนี้ไปใช้ในการแก้ปัญหาได้

ความรู้ ทักษะ และความสามารถเบื้องต้นที่จำเป็น:

กำหนดค่าของฟังก์ชันด้วยค่าของอาร์กิวเมนต์ด้วยวิธีต่างๆ ในการระบุฟังก์ชัน

สร้างกราฟของฟังก์ชันที่ศึกษา

อธิบายพฤติกรรมและคุณสมบัติของฟังก์ชันโดยใช้กราฟและในกรณีที่ง่ายที่สุดให้ใช้สูตร ค้นหาค่าที่ใหญ่ที่สุดและน้อยที่สุดจากกราฟของฟังก์ชัน

คำอธิบายโดยใช้ฟังก์ชันของการขึ้นต่อกันต่างๆ แทนในรูปแบบกราฟิก การตีความกราฟ

ส่วนหลัก

ส่วนทางทฤษฎี

เนื่องจากกราฟเริ่มต้นของฟังก์ชัน y = f(x) ผมจะเลือกฟังก์ชันกำลังสอง ย = x 2 . ฉันจะพิจารณากรณีของการเปลี่ยนแปลงกราฟนี้ที่เกี่ยวข้องกับการเปลี่ยนแปลงในสูตรที่กำหนดฟังก์ชันนี้และสรุปผลสำหรับฟังก์ชันใดๆ

1. ฟังก์ชัน y = f(x) + a

ในสูตรใหม่ ค่าฟังก์ชัน (พิกัดของจุดกราฟ) จะเปลี่ยนตามตัวเลข a เทียบกับค่าฟังก์ชัน "เก่า" สิ่งนี้นำไปสู่การถ่ายโอนกราฟฟังก์ชันตามแนวแกน OY แบบขนาน:

ขึ้นถ้า > 0; ลงถ้าก< 0.

บทสรุป

ดังนั้น กราฟของฟังก์ชัน y=f(x)+a จะได้มาจากกราฟของฟังก์ชัน y=f(x) โดยใช้การแปลแบบขนานตามแนวแกนพิกัดโดยหน่วยขึ้นถ้า a > 0 และโดยหน่วยลง ถ้าก< 0.

2. ฟังก์ชัน y = f(x-a)

ในสูตรใหม่ ค่าอาร์กิวเมนต์ (abscissas ของจุดกราฟ) จะเปลี่ยนตามตัวเลข a เทียบกับค่าอาร์กิวเมนต์ "เก่า" สิ่งนี้นำไปสู่การถ่ายโอนกราฟฟังก์ชันไปตามแกน OX แบบขนาน: ไปทางขวา ถ้า a< 0, влево, если a >0.

บทสรุป

ซึ่งหมายความว่ากราฟของฟังก์ชัน y= f(x - a) ได้มาจากกราฟของฟังก์ชัน y=f(x) โดยการแปลแบบขนานไปตามแกน abscissa ด้วยหน่วยทางด้านซ้ายถ้า a > 0 และโดย หน่วยทางขวาถ้าก< 0.

3. ฟังก์ชัน y = k f(x) โดยที่ k > 0 และ k ≠ 1

ในสูตรใหม่ ค่าฟังก์ชัน (พิกัดของจุดกราฟ) เปลี่ยนแปลง k ครั้ง เทียบกับค่าฟังก์ชัน "เก่า" สิ่งนี้นำไปสู่: 1) “การยืด” จากจุด (0; 0) ไปตามแกน OY ด้วยปัจจัย k ถ้า k > 1, 2) “การบีบอัด” ไปยังจุด (0; 0) ไปตามแกน OY โดย ตัวประกอบของ ถ้า 0< k < 1.

บทสรุป

ดังนั้น: ในการสร้างกราฟของฟังก์ชัน y = kf(x) โดยที่ k > 0 และ k ≠ 1 คุณต้องคูณพิกัดของจุดของกราฟที่กำหนดของฟังก์ชัน y = f(x) ด้วย k การเปลี่ยนแปลงดังกล่าวเรียกว่าการยืดจากจุด (0; 0) ไปตามแกน OY คูณ k คูณถ้า k > 1; การบีบอัดไปที่จุด (0; 0) ตามแนวแกน OY คูณด้วย 0< k < 1.

4. ฟังก์ชัน y = f(kx) โดยที่ k > 0 และ k ≠ 1

ในสูตรใหม่ ค่าอาร์กิวเมนต์ (abscissas ของจุดกราฟ) เปลี่ยนแปลง k ครั้งเมื่อเปรียบเทียบกับค่าอาร์กิวเมนต์ "เก่า" สิ่งนี้นำไปสู่: 1) “ยืด” จากจุด (0; 0) ไปตามแกน OX 1/k คูณ ถ้า 0< k < 1; 2) «сжатию» к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

บทสรุป

ดังนั้น: ในการสร้างกราฟของฟังก์ชัน y = f(kx) โดยที่ k > 0 และ k ≠ 1 คุณต้องคูณ abscissa ของจุดของกราฟที่กำหนดของฟังก์ชัน y=f(x) ด้วย k . การเปลี่ยนแปลงดังกล่าวเรียกว่าการยืดจากจุด (0; 0) ไปตามแกน OX 1/k คูณ ถ้า 0< k < 1, сжатием к точке (0; 0) вдоль оси OX. в k раз, если k > 1.

5. ฟังก์ชัน y = - f (x)

ในสูตรนี้ ค่าฟังก์ชัน (พิกัดของจุดกราฟ) จะกลับกัน การเปลี่ยนแปลงนี้นำไปสู่การแสดงกราฟดั้งเดิมของฟังก์ชันที่สัมพันธ์กับแกน Ox อย่างสมมาตร

บทสรุป

ในการพล็อตกราฟของฟังก์ชัน y = - f (x) คุณต้องมีกราฟของฟังก์ชัน y= f(x)

สะท้อนรอบแกน OX อย่างสมมาตร การแปลงนี้เรียกว่าการแปลงสมมาตรรอบแกน OX

6. ฟังก์ชัน y = ฉ (-x)

ในสูตรนี้ ค่าของอาร์กิวเมนต์ (abscissa ของจุดกราฟ) จะถูกกลับรายการ การเปลี่ยนแปลงนี้นำไปสู่การแสดงกราฟดั้งเดิมของฟังก์ชันที่สัมพันธ์กับแกน OY อย่างสมมาตร

ตัวอย่างของฟังก์ชัน y = - x² การแปลงนี้ไม่สังเกตเห็นได้ชัดเจน เนื่องจากฟังก์ชันนี้เป็นเลขคู่และกราฟจะไม่เปลี่ยนแปลงหลังการแปลง การเปลี่ยนแปลงนี้สามารถมองเห็นได้เมื่อฟังก์ชันเป็นเลขคี่ และเมื่อไม่เป็นเลขคู่หรือเลขคี่

7. ฟังก์ชัน y = |f(x)|

ในสูตรใหม่ ค่าฟังก์ชัน (พิกัดของจุดกราฟ) อยู่ใต้เครื่องหมายโมดูลัส สิ่งนี้นำไปสู่การหายไปของส่วนต่างๆ ของกราฟของฟังก์ชันดั้งเดิมที่มีลำดับเชิงลบ (เช่น ส่วนที่อยู่ในระนาบครึ่งล่างสัมพันธ์กับแกน Ox) และการแสดงส่วนเหล่านี้อย่างสมมาตรสัมพันธ์กับแกน Ox

8. ฟังก์ชัน y= ฉ (|x|)

ในสูตรใหม่ ค่าอาร์กิวเมนต์ (abscissas ของจุดกราฟ) อยู่ใต้เครื่องหมายโมดูลัส สิ่งนี้นำไปสู่การหายไปของส่วนต่างๆ ของกราฟของฟังก์ชันดั้งเดิมที่มีจุดตัดเป็นลบ (เช่น ซึ่งอยู่ในระนาบครึ่งซ้ายสัมพันธ์กับแกน OY) และการแทนที่ด้วยส่วนของกราฟต้นฉบับที่มีความสมมาตรสัมพันธ์กับแกน OY .

ส่วนการปฏิบัติ

ลองดูตัวอย่างบางส่วนของการประยุกต์ใช้ทฤษฎีข้างต้น

ตัวอย่างที่ 1

สารละลาย.มาแปลงสูตรนี้กัน:

1) มาสร้างกราฟของฟังก์ชันกัน

ตัวอย่างที่ 2

สร้างกราฟฟังก์ชันที่กำหนดโดยสูตร

สารละลาย. ให้เราแปลงสูตรนี้โดยแยกกำลังสองของทวินามออกจากตรีโกณมิติกำลังสองนี้:

1) มาสร้างกราฟของฟังก์ชันกัน

2) ทำการถ่ายโอนกราฟที่สร้างขึ้นไปยังเวกเตอร์แบบขนาน

ตัวอย่างที่ 3

งานจากการสอบ Unified State การสร้างกราฟฟังก์ชันทีละส่วน

กราฟของฟังก์ชัน กราฟของฟังก์ชัน y=|2(x-3)2-2|; 1

ขึ้นอยู่กับเงื่อนไขของกระบวนการทางกายภาพ ปริมาณบางปริมาณใช้ค่าคงที่และเรียกว่าค่าคงที่ ส่วนปริมาณอื่น ๆ เปลี่ยนแปลงภายใต้เงื่อนไขบางประการและเรียกว่าตัวแปร

การศึกษาสภาพแวดล้อมอย่างรอบคอบแสดงให้เห็นว่าปริมาณทางกายภาพขึ้นอยู่กับปริมาณอื่น กล่าวคือ การเปลี่ยนแปลงในปริมาณหนึ่งจะนำมาซึ่งการเปลี่ยนแปลงในปริมาณอื่นๆ ด้วย

การวิเคราะห์ทางคณิตศาสตร์เกี่ยวข้องกับการศึกษาความสัมพันธ์เชิงปริมาณระหว่างปริมาณที่ต่างกันออกไป โดยสรุปจากความหมายทางกายภาพที่เฉพาะเจาะจง แนวคิดพื้นฐานของการวิเคราะห์ทางคณิตศาสตร์ประการหนึ่งคือแนวคิดเรื่องฟังก์ชัน

พิจารณาองค์ประกอบของเซตและองค์ประกอบของเซต
(รูปที่ 3.1)

หากมีการสร้างความสอดคล้องกันระหว่างองค์ประกอบของเซต
และ ในรูปแบบของกฎเกณฑ์ จากนั้นพวกเขาจะทราบว่ามีการกำหนดฟังก์ชันแล้ว
.

คำนิยาม 3.1. การโต้ตอบ ซึ่งเชื่อมโยงกับแต่ละองค์ประกอบ ไม่ใช่ชุดเปล่า
องค์ประกอบบางอย่างที่กำหนดไว้อย่างดี ไม่ใช่ชุดเปล่า เรียกว่าฟังก์ชันหรือการแมป
วี .

แสดงเป็นสัญลักษณ์
วี เขียนดังนี้:

.

ในขณะเดียวกันก็มากมาย
เรียกว่าโดเมนของคำจำกัดความของฟังก์ชันและเขียนแทนด้วย
.

ในทางกลับกันหลายคน เรียกว่าช่วงของค่าของฟังก์ชันและแสดงแทน
.

นอกจากนี้ก็ควรสังเกตด้วยว่าองค์ประกอบของชุด
เรียกว่าตัวแปรอิสระ องค์ประกอบของเซต เรียกว่าตัวแปรตาม

วิธีการระบุฟังก์ชัน

สามารถระบุฟังก์ชันได้ด้วยวิธีหลักๆ ดังต่อไปนี้: แบบตาราง กราฟิก และการวิเคราะห์

หากขึ้นอยู่กับข้อมูลการทดลองแล้ว ตารางจะถูกคอมไพล์ที่มีค่าของฟังก์ชันและค่าอาร์กิวเมนต์ที่เกี่ยวข้อง ดังนั้นวิธีการระบุฟังก์ชันนี้เรียกว่าตาราง

ในเวลาเดียวกันหากการศึกษาผลการทดลองบางส่วนแสดงบนเครื่องบันทึก (ออสซิลโลสโคปเครื่องบันทึก ฯลฯ ) จะมีการสังเกตว่าฟังก์ชั่นนั้นถูกระบุเป็นกราฟิก

วิธีที่พบบ่อยที่สุดคือวิธีวิเคราะห์ในการระบุฟังก์ชัน เช่น วิธีการเชื่อมโยงตัวแปรอิสระและตัวแปรตามโดยใช้สูตร ในกรณีนี้ ขอบเขตของคำจำกัดความของฟังก์ชันมีบทบาทสำคัญ:

แตกต่างกันแม้ว่าจะได้รับจากความสัมพันธ์เชิงวิเคราะห์ที่เหมือนกันก็ตาม

หากระบุเฉพาะสูตรฟังก์ชัน
จากนั้นเราจะพิจารณาว่าโดเมนของคำจำกัดความของฟังก์ชันนี้เกิดขึ้นพร้อมกับชุดของค่าเหล่านั้นของตัวแปร ซึ่งการแสดงออก
สมเหตุสมผล ในเรื่องนี้ ปัญหาในการค้นหาโดเมนของคำจำกัดความของฟังก์ชันมีบทบาทพิเศษ

งาน 3.1. ค้นหาโดเมนของฟังก์ชัน

สารละลาย

เทอมแรกจะใช้ค่าจริงเมื่อใด
และครั้งที่สองที่ ดังนั้น ในการค้นหาโดเมนของคำจำกัดความของฟังก์ชันที่กำหนด จำเป็นต้องแก้ระบบอสมการ:

ผลที่ได้คือวิธีแก้ปัญหาของระบบดังกล่าวคือ ดังนั้น โดเมนของคำจำกัดความของฟังก์ชันคือส่วน
.

การแปลงกราฟฟังก์ชันที่ง่ายที่สุด

การสร้างกราฟฟังก์ชันสามารถทำได้ง่ายขึ้นอย่างมากหากคุณใช้กราฟที่รู้จักกันดีของฟังก์ชันพื้นฐานเบื้องต้น ฟังก์ชันต่อไปนี้เรียกว่าฟังก์ชันพื้นฐานหลัก:

1) ฟังก์ชั่นพลังงาน
ที่ไหน
;

2) ฟังก์ชันเลขชี้กำลัง
ที่ไหน
และ
;

3)ฟังก์ชันลอการิทึม
, ที่ไหน - จำนวนบวกใดๆ ที่ไม่ใช่หนึ่ง:
และ
;

4) ฟังก์ชันตรีโกณมิติ




;
.

5) ฟังก์ชันตรีโกณมิติผกผัน
;
;
;
.

ฟังก์ชันพื้นฐานคือฟังก์ชันที่ได้รับจากฟังก์ชันพื้นฐานพื้นฐานโดยใช้การดำเนินการทางคณิตศาสตร์สี่รายการและการซ้อนทับที่ใช้จำนวนครั้งจำกัด

การแปลงทางเรขาคณิตอย่างง่ายยังทำให้กระบวนการสร้างกราฟของฟังก์ชันง่ายขึ้นอีกด้วย การแปลงเหล่านี้ขึ้นอยู่กับข้อความต่อไปนี้:

กราฟของฟังก์ชัน y=f(x+a) คือกราฟ y=f(x) ที่ถูกเลื่อน (สำหรับ a >0 ไปทางซ้าย สำหรับ a< 0 вправо) на |a| единиц параллельно осиOx.

กราฟของฟังก์ชัน y=f(x) +b คือกราฟของ y=f(x) เลื่อน (ที่ b>0 ขึ้นไป ที่ b< 0 вниз) на |b| единиц параллельно осиOy.

กราฟของฟังก์ชัน y = mf(x) (m0) คือกราฟของ y = f(x) ยืดออก (ที่ m>1) m ครั้งหรือถูกบีบอัด (ที่ 0

กราฟของฟังก์ชัน y = f(kx) คือกราฟของ y = f(x) ที่ถูกบีบอัด (สำหรับ k >1) k ครั้งหรือยืดออก (สำหรับ 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx) есть зеркальное отображение графика y = f(–kx) от оси Oy.

สมมติฐาน: หากคุณศึกษาการเคลื่อนที่ของกราฟระหว่างการสร้างสมการฟังก์ชัน คุณจะสังเกตเห็นว่ากราฟทั้งหมดเป็นไปตามกฎทั่วไป ดังนั้นจึงเป็นไปได้ที่จะกำหนดกฎทั่วไปโดยไม่คำนึงถึงฟังก์ชัน ซึ่งไม่เพียงแต่จะอำนวยความสะดวกในการสร้าง กราฟของฟังก์ชันต่างๆ แต่ยังใช้ในการแก้ปัญหาด้วย

วัตถุประสงค์: เพื่อศึกษาการเคลื่อนที่ของกราฟของฟังก์ชัน:

1) งานคือการศึกษาวรรณกรรม

2) เรียนรู้การสร้างกราฟของฟังก์ชันต่างๆ

3) เรียนรู้การแปลงกราฟของฟังก์ชันเชิงเส้น

4) พิจารณาประเด็นการใช้กราฟในการแก้ปัญหา

วัตถุประสงค์ของการศึกษา: กราฟฟังก์ชัน

หัวข้อวิจัย: การเคลื่อนที่ของกราฟฟังก์ชัน

ความเกี่ยวข้อง: ตามกฎแล้วการสร้างกราฟของฟังก์ชันจะใช้เวลามากและต้องอาศัยความใส่ใจของนักเรียน แต่เมื่อรู้กฎสำหรับการแปลงกราฟของฟังก์ชันและกราฟของฟังก์ชันพื้นฐาน คุณจะสามารถสร้างกราฟของฟังก์ชันได้อย่างรวดเร็วและง่ายดาย ซึ่งจะช่วยให้คุณไม่เพียงแต่ทำงานให้สำเร็จเพื่อสร้างกราฟของฟังก์ชันเท่านั้น แต่ยังช่วยแก้ปัญหาที่เกี่ยวข้องด้วย (เพื่อค้นหาค่าสูงสุด (ความสูงขั้นต่ำของเวลาและจุดนัดพบ))

โครงการนี้เป็นประโยชน์กับนักเรียนทุกคนที่โรงเรียน

การทบทวนวรรณกรรม:

วรรณกรรมกล่าวถึงวิธีการสร้างกราฟของฟังก์ชันต่างๆ รวมถึงตัวอย่างการแปลงกราฟของฟังก์ชันเหล่านี้ กราฟของฟังก์ชันหลักเกือบทั้งหมดใช้ในกระบวนการทางเทคนิคต่างๆ ซึ่งช่วยให้คุณเห็นภาพการไหลของกระบวนการได้ชัดเจนยิ่งขึ้นและตั้งโปรแกรมผลลัพธ์ได้

ฟังก์ชั่นถาวร ฟังก์ชันนี้ได้มาจากสูตร y = b โดยที่ b คือตัวเลขจำนวนหนึ่ง กราฟของฟังก์ชันคงที่จะเป็นเส้นตรงขนานกับเส้น Abscissa และผ่านจุด (0; b) บนพิกัด กราฟของฟังก์ชัน y = 0 คือแกน x

ประเภทของฟังก์ชัน 1 สัดส่วนโดยตรง ฟังก์ชันนี้กำหนดโดยสูตร y = kx โดยที่ค่าสัมประสิทธิ์ของสัดส่วน k ≠ 0 กราฟของสัดส่วนโดยตรงคือเส้นตรงที่ลากผ่านจุดกำเนิด

ฟังก์ชันเชิงเส้น ฟังก์ชันดังกล่าวได้มาจากสูตร y = kx + b โดยที่ k และ b เป็นจำนวนจริง กราฟของฟังก์ชันเชิงเส้นจะเป็นเส้นตรง

กราฟของฟังก์ชันเชิงเส้นสามารถตัดกันหรือขนานกันได้

ดังนั้น เส้นกราฟของฟังก์ชันเชิงเส้น y = k 1 x + b 1 และ y = k 2 x + b 2 ตัดกันถ้า k 1 ≠ k 2 ; ถ้า k 1 = k 2 แล้วเส้นตรงจะขนานกัน

2สัดส่วนผกผันคือฟังก์ชันที่กำหนดโดยสูตร y = k/x โดยที่ k ≠ 0 K เรียกว่าสัมประสิทธิ์สัดส่วนผกผัน กราฟของสัดส่วนผกผันคือไฮเปอร์โบลา

ฟังก์ชัน y = x 2 แสดงด้วยกราฟที่เรียกว่าพาราโบลา: ในช่วงเวลา [-~; 0] ฟังก์ชันจะลดลง ตามช่วงเวลาที่ฟังก์ชันเพิ่มขึ้น

ฟังก์ชัน y = x 3 จะเพิ่มขึ้นตามเส้นจำนวนทั้งหมด และแสดงเป็นกราฟด้วยพาราโบลาลูกบาศก์

ฟังก์ชันยกกำลังพร้อมเลขชี้กำลังธรรมชาติ ฟังก์ชันนี้ได้มาจากสูตร y = x n โดยที่ n คือจำนวนธรรมชาติ กราฟของฟังก์ชันยกกำลังที่มีเลขชี้กำลังตามธรรมชาติจะขึ้นอยู่กับ n ตัวอย่างเช่น ถ้า n = 1 กราฟจะเป็นเส้นตรง (y = x) ถ้า n = 2 กราฟจะเป็นพาราโบลา เป็นต้น

ฟังก์ชันยกกำลังที่มีเลขชี้กำลังจำนวนเต็มลบแสดงด้วยสูตร y = x -n โดยที่ n คือจำนวนธรรมชาติ ฟังก์ชันนี้ถูกกำหนดไว้สำหรับ x ≠ 0 ทั้งหมด กราฟของฟังก์ชันยังขึ้นอยู่กับเลขชี้กำลัง n ด้วย

ฟังก์ชันยกกำลังที่มีเลขชี้กำลังเศษส่วนบวก ฟังก์ชันนี้แสดงด้วยสูตร y = x r โดยที่ r คือเศษส่วนบวกที่ลดไม่ได้ ฟังก์ชันนี้ไม่เป็นคู่หรือคี่ด้วย

กราฟเส้นที่แสดงความสัมพันธ์ระหว่างตัวแปรตามและตัวแปรอิสระบนระนาบพิกัด กราฟทำหน้าที่แสดงองค์ประกอบเหล่านี้ด้วยสายตา

ตัวแปรอิสระคือตัวแปรที่สามารถรับค่าใดๆ ในโดเมนของนิยามฟังก์ชันได้ (โดยที่ฟังก์ชันที่กำหนดมีความหมาย (ไม่สามารถหารด้วยศูนย์ได้))

เพื่อสร้างกราฟของฟังก์ชันที่คุณต้องการ

1) ค้นหา VA (ช่วงของค่าที่ยอมรับได้)

2) รับค่าที่กำหนดเองหลายค่าสำหรับตัวแปรอิสระ

3) ค้นหาค่าของตัวแปรตาม

4) สร้างระนาบพิกัดและทำเครื่องหมายจุดเหล่านี้บนระนาบนั้น

5) เชื่อมต่อเส้นของพวกเขาหากจำเป็น ให้ตรวจสอบกราฟผลลัพธ์ การแปลงกราฟของฟังก์ชันพื้นฐาน

การแปลงกราฟ

ในรูปแบบที่บริสุทธิ์ ฟังก์ชันพื้นฐานขั้นพื้นฐานนั้น น่าเสียดายที่ไม่ธรรมดานัก บ่อยครั้งที่คุณต้องจัดการกับฟังก์ชันพื้นฐานที่ได้รับจากฟังก์ชันพื้นฐานโดยการเพิ่มค่าคงที่และสัมประสิทธิ์ กราฟของฟังก์ชันดังกล่าวสามารถสร้างขึ้นได้โดยใช้การแปลงทางเรขาคณิตกับกราฟของฟังก์ชันพื้นฐานพื้นฐานที่เกี่ยวข้อง (หรือเปลี่ยนไปใช้ระบบพิกัดใหม่) ตัวอย่างเช่น สูตรฟังก์ชันกำลังสองคือสูตรพาราโบลากำลังสอง ซึ่งบีบอัดสามครั้งสัมพันธ์กับแกนกำหนด แสดงอย่างสมมาตรสัมพันธ์กับแกนแอบซิสซา เลื่อนไปทางทิศทางของแกนนี้ 2/3 หน่วย และเลื่อนไปตามแกนกำหนด 2 หน่วย

มาทำความเข้าใจการเปลี่ยนแปลงทางเรขาคณิตของกราฟของฟังก์ชันทีละขั้นตอนโดยใช้ตัวอย่างที่เฉพาะเจาะจง

การใช้การแปลงทางเรขาคณิตของกราฟของฟังก์ชัน f(x) สามารถสร้างกราฟของฟังก์ชันใดๆ ของสูตรในรูปแบบได้ โดยที่สูตรคือค่าสัมประสิทธิ์การบีบอัดหรือการยืดตามแนวแกน oy และแกนวัว ตามลำดับ โดยมีเครื่องหมายลบอยู่ด้านหน้า ของสูตรและค่าสัมประสิทธิ์ของสูตรบ่งชี้ถึงการแสดงกราฟแบบสมมาตรสัมพันธ์กับแกนพิกัด a และ b กำหนดการเปลี่ยนแปลงที่สัมพันธ์กับแกนแอบซิสซาและแกนพิกัดตามลำดับ

ดังนั้น การแปลงทางเรขาคณิตของกราฟของฟังก์ชันจึงมีสามประเภท:

ประเภทแรกคือการปรับขนาด (การบีบอัดหรือการยืด) ตามแนว abscissa และกำหนดแกน

ความจำเป็นในการปรับขนาดจะถูกระบุด้วยค่าสัมประสิทธิ์สูตรอื่นที่มากกว่าหนึ่ง หากตัวเลขน้อยกว่า 1 แสดงว่ากราฟถูกบีบอัดโดยสัมพันธ์กับ oy และยืดออกโดยสัมพันธ์กับวัว หากตัวเลขมากกว่า 1 เราจะยืดไปตามแกนกำหนด และบีบอัดตามแนวแกนแอบซิสซา

ประเภทที่สองคือการแสดงผลแบบสมมาตร (กระจกเงา) ที่สัมพันธ์กับแกนพิกัด

ความจำเป็นในการแปลงนี้ระบุด้วยเครื่องหมายลบหน้าค่าสัมประสิทธิ์ของสูตร (ในกรณีนี้ เราจะแสดงกราฟแบบสมมาตรเกี่ยวกับแกนวัว) และสูตร (ในกรณีนี้ เราจะแสดงกราฟแบบสมมาตรเกี่ยวกับ oy แกน). หากไม่มีเครื่องหมายลบ ขั้นตอนนี้จะถูกข้ามไป