Mekkora a kocka kmo sík szerinti metszete? „Kocka metszete síkkal és gyakorlati alkalmazása a feladatokban”

Válasszon ki egy poliédert és a nehézségi szintet

Paralelepipedon.

Tetraéder.

Kocka A szint.

A szint.

Paralelepipedon.

Kocka B szint.

B szint.

Tetraéder.

B szint.

Paralelepipedon.

Tetraéder.

Kocka C szint.

C szint.

Kocka A szint.

pont M, H és K, ahol KЄ(DCC 1 D 1 ).

V 1

VAL VEL 1

D 1

Segítség

a) sík BB éllel 1 ; b) sík (SS 1 D).

Kocka B szint.

V 1

VAL VEL 1

D 1

Segítség

Kocka C szint.

Szerkesszük meg a kocka egy szakaszát, amelyen egy sík halad a K, E és M pontokon keresztül (M Є AB). Ezután keresse meg a BB egyenes metszéspontját 1 ezzel a géppel.

V 1

VAL VEL 1

D 1

Kocka A szint.

Szerkesszük meg az áthaladó tetraéder keresztmetszetét!

pont M, H és K, ahol KЄ(DCC 1 D 1 ).

V 1

VAL VEL 1

EP ll MN

D 1

Kocka B szint.

V 1

VAL VEL 1

D 1

AN ll KE

Szerkesszünk meg egy kocka szakaszt, amelyen egy sík halad át

Az A, K és E pontok. Határozzuk meg ennek metszésvonalát!

a) sík BB éllel 1 ; b) sík (SS 1 D).

Kocka C szint.

Szerkesszük meg a kocka olyan szakaszát, amelyik a K, E és M pontokon áthalad (M Є AB). Ezután keresse meg a BB1 egyenes metszéspontját ezzel a síkkal.

V 1

VAL VEL 1

D 1

PHKERF– kötelező szakasz

A szint. AA bordákon 1 és A 1 D 1 1 1 = 6, A 1 D 1 = 8, AB = 4 cm.

Segítség

B szint.

Segítség

LevelC. A paralelepipedon élein három S, R és L pont van megadva. Szerkesszük meg a paralelepipedon metszetét az SRL sík segítségével.

Segítség

A szint. AA bordákon 1 és A 1 D 1 a paralelepipedonból az S és R felezőpontokat rendre felvesszük. Szerkesszük meg a paralelepipedon metszetét az SRВ sík segítségével 1 és keresse meg a keresztmetszeti területet, ha AA 1 = 6, A 1 D 1 = 8, AB = 4 cm.

jegyzet

Alkalmazza Heron képletét.

B szint

SRELZX– kötelező szakasz

C szint.

Tetraéder.

A szint.

Segítség

Tetraéder.

Szerkesszük meg a tetraéder metszetét, amelyen egy sík halad

B szint.

Segítség

A tetraéderben a lapok (STA) és (ATV) magasságában a K és M pontokat veszik,

és az E pont az (ABC) síkban fekszik. Rajzolj egy tetraéder keresztmetszetét!

áthaladva ezeken a pontokon.

Tetraéder.

C szint.

Segítség

Szerkesszük meg a tetraéder metszetét, amelyen egy sík halad

az ST, SA bordák közepén és a KЄTV ponton keresztül. Határozza meg a nézetet

szakaszban kapott négyszög.

Tetraéder.

A szint.

Tetraéder.

Szerkesszük meg a tetraéder metszetét, amelyen egy sík halad

B szint.

az M és H pontokon és a KЄ(ABC) ponton keresztül.

MNRE– kötelező szakasz

Feladatok a kocka szakaszainak felépítésérőlD1
C1
E
A1
B1
D
A
F
B
VAL VEL

Ellenőrző munka.

1 lehetőség
2. lehetőség
1. tetraéder
1. paralelepipedon
2. A paralelepipedon tulajdonságai

A kocka vágási síkja minden olyan sík, amelynek mindkét oldalán egy adott kocka pontjai vannak.

Metsző
a sík mentén metszi a kocka lapjait
szegmensek.
Egy sokszög, amelynek oldalai vannak
Ezeket a szakaszokat a kocka szakaszának nevezzük.
A kocka szakaszai lehetnek háromszögek,
négyszögek, ötszögek és
hatszögek.
A szakaszok építésénél ezt figyelembe kell venni
tény, hogy ha egy vágósík metszi kettőt
bizonyos szegmensek mentén átellenes oldalak, majd
ezek a szegmensek párhuzamosak. (Mondd el miért).

B1
C1
D1
A1
M
K
FONTOS!
B
VAL VEL
D
Ha a vágási sík metszi
ellentétes élek, majd azt
K DCC1
párhuzamosan metszi őket
M BCC1
szegmensek.

három adott pont, amelyek az élek felezőpontjai. Keresse meg a szakasz kerületét, ha az él

Szerkesszük meg a kocka azon szakaszát, amelyen egy sík halad át
három adott pont, amelyek az élek felezőpontjai.
Határozzuk meg a szakasz kerületét, ha a kocka éle egyenlő a-val.
D1
N
K
A1
D
A
C1
B1
M
VAL VEL
B

Szerkesszük meg a kocka olyan szakaszát, amely három megadott ponton halad át, amelyek a csúcsai. Határozza meg a szakasz kerületét, ha a kocka éle

Szerkesszük meg a kocka azon szakaszát, amelyen egy sík halad át
három adott pont, amelyek a csúcsai. megtalálja
a szakasz kerülete, ha a kocka éle egyenlő a.
D1
C1
A1
B1
D
A
VAL VEL
B

D1
C1
A1
M
B1
D
A
VAL VEL
B

Szerkesszük meg a kocka olyan szakaszát, amelynek síkja három megadott ponton halad át. Határozzuk meg a szakasz kerületét, ha a kocka éle egyenlő a-val.

D1
C1
A1
B1
N
D
A
VAL VEL
B

Szerkesszük meg a kocka olyan szakaszát, amely három megadott ponton halad át, amelyek az éleinek felezőpontjai.

C1
D1
B1
A1
K
D
VAL VEL
N
E
A
M
B

Feladatok a kocka szakaszainak felépítésérőlD1
C1
E
A1
B1
D
A
F
B
VAL VEL

Ellenőrző munka.

1 lehetőség
2. lehetőség
1. tetraéder
1. paralelepipedon
2. A paralelepipedon tulajdonságai

A kocka vágási síkja minden olyan sík, amelynek mindkét oldalán egy adott kocka pontjai vannak.

B1
C1
D1
A1
M
K
FONTOS!
B
VAL VEL
D
Ha a vágási sík metszi
ellentétes élek, majd azt
K DCC1
párhuzamosan metszi őket
M BCC1
szegmensek.

három adott pont, amelyek az élek felezőpontjai. Keresse meg a szakasz kerületét, ha az él

Szerkesszük meg a kocka olyan szakaszát, amely három megadott ponton halad át, amelyek a csúcsai. Határozza meg a szakasz kerületét, ha a kocka éle

Szerkesszük meg a kocka azon szakaszát, amelyen egy sík halad át
három adott pont, amelyek a csúcsai. megtalálja
a szakasz kerülete, ha a kocka éle egyenlő a.
D1
C1
A1
B1
D
A
VAL VEL
B

D1
C1
A1
M
B1
D
A
VAL VEL
B

Szerkesszük meg a kocka olyan szakaszát, amelynek síkja három megadott ponton halad át. Határozzuk meg a szakasz kerületét, ha a kocka éle egyenlő a-val.

D1
C1
A1
B1
N
D
A
VAL VEL
B

Szerkesszük meg a kocka olyan szakaszát, amely három megadott ponton halad át, amelyek az éleinek felezőpontjai.

C1
D1
B1
A1
K
D
VAL VEL
N
E
A
M
B

І-ІІІ szintű általános oktatási iskola 2. sz

Kirovszkoje városi közigazgatás oktatási osztálya

„Kocka szakasz repülővel

és gyakorlati alkalmazásukat problémákban.”

Matektanár készítette

tanár-módszerész

Chumakova G.V.

2015

Bevezetés:

Mind a középiskolai geometria-tanfolyamokon, mind a különböző szintű vizsgákon jelentős helyet foglalnak el a poliéder szakaszok megalkotásával kapcsolatos problémák. Az ilyen típusú problémák megoldása hozzájárul a sztereometria axiómáinak asszimilációjához, az ismeretek és készségek rendszerezéséhez, a térmegértés és a konstruktív készségek fejlesztéséhez. A szakaszok építésével járó problémák megoldása során felmerülő nehézségek jól ismertek.

A metszetkészítés módszerét alkotó fő műveletek az egyenes és a sík metszéspontjának megkeresése, két sík metszésvonalának megalkotása, egy síkkal párhuzamos egyenes és a síkra merőleges egyenes megalkotása. repülőgép.

Szemléltetem egy szakasz felépítését egy iskolai matematika kurzus egyik feladatával:

№1. Építsd meg a kocka legalább két szakaszátABCDA 1 B 1 C 1 D 1 repülőgép AM 1 C, ha M pont 1 a BB szakasz mentén mozog 1 B-ből B-be 1 . Határozzuk meg az M pontból húzott szakasz magasságmérésének határait! 1 .

Megoldás: Készítsünk két szükséges szakaszt az M pont alapján 1 közelebb a B ponthoz és az M ponthoz 2 közelebb B-hez 1 . Az ábrán mindkét szakasz látható A mozgás elején, amikor az M pont 1 most távolodott el a B ponttól 1 , a metszet egy háromszög AC alappal és M magassággal 1 O, ami valamivel nagyobb, mint a BO szegmens, azaz.
Ha az M pont 1 M pozíciót tölt be 2 nagyon közel található a B ponthoz 1 , Azt AM 2 C majdnem egybeesik AB 1 C, magassága pedig M 1 O – B szegmenssel 1 Ó, akinek a hossza
(OB 1 =
=
).

Innen a folytonosság érdekében a következő következtetést vonjuk le: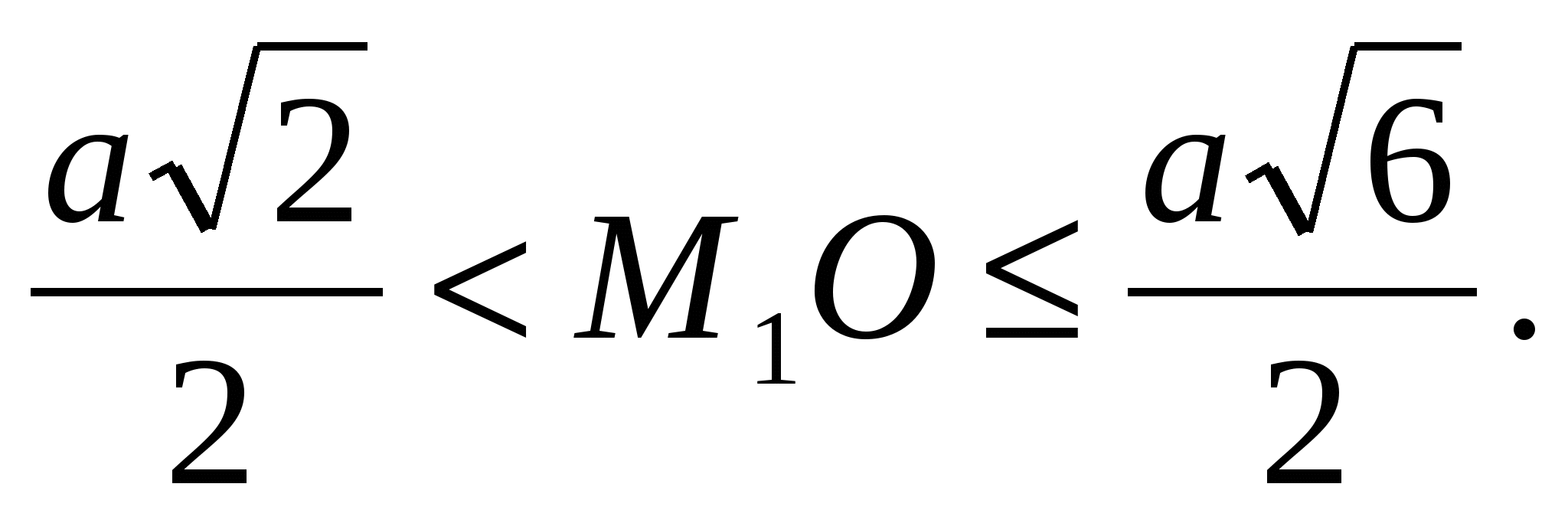

Különösen azt kell nézni, hogy mi történik, ha az M 1 pont a B csúcs pozícióját veszi fel.

№2. Szerkessze meg a kocka olyan szakaszát, amely a kocka élein fekvő három A 1, E és L ponton áthalad.

Az A 1 ADD 1 és DD 1 C 1 C lapok síkjai a DD 1 egyenes mentén, az A 1 B 1 C 1 D 1 u DD 1 C 1 C lapok síkjai pedig a D 1 egyenes mentén metszik egymást. C 1. Az A és E pontok összekapcsolásával megkapjuk a vágási sík metszésvonalát az AA 1 D 1 D lap síkjával, majd ezt folytatva megtaláljuk az N pontot, amely három síkhoz tartozik: a vágási síkhoz és a az arcok síkjai AA 1 D 1 D u DD 1 C 1 C.

Hasonlóképpen találjuk az M pontot, amely három síkra közös: a metszetsíkra és az A 1 B 1 C 1 D 1 u DD 1 C 1 C lapok síkjaira. Így az N u M pontok a vágási síkhoz és a DD 1 C 1 C síkhoz tartoznak; Az MN egyenes a metszősík metszésvonala a DD 1 C 1 C lap síkjával, F és K pedig a CD u CC 1 kocka éleivel való metszéspontjai. Az A 1 , E , F , K u L pontokat következetesen egyenesekkel összekötve megkapjuk az A ötszöget! EFKL, amely megadja nekünk a kívánt részt.

Ha egy kocka szakaszt sík segítségével készítünk x a szakasz pontjainak tetszőleges elrendezésével az eredmény: háromszög, trapéz, téglalap, ötszög vagy hatszög. Természetesen felmerült a kérdés, hogy a szakasz típusa hogyan függ a szakaszt meghatározó pontok elhelyezkedésétől

Úgy döntöttem, hogy elvégzek egy tanulmányt, hogy megtudjam.

Egy kocka metszeteinek szerkesztése sík mentén, ha adott három, egy csúcsú élekhez tartozó pont.

Három A 1 , D , C 1 pontot veszünk fel, amelyek a D 1 csúcshoz tartoznak, és maguk a kocka csúcsai.

A keresztmetszet egy egyenlő oldalú háromszöget eredményez, mivel A 1 C 1, A 1 D u DC 1 ennek a kockának a lapjainak átlói.

Három pont: A 1 u C 1 a kocka csúcsai, az F pont pedig a DD 1 kocka éléhez tartozik. A pontok a D 1 csúcsból kilépő egyenesekhez tartoznak.

A keresztmetszet egy egyenlő szárú háromszöget eredményez, mivel F egyenlő távolságra van az A 1 u C 1 pontoktól.

Három pont: A 1 u C 1 a kocka csúcsai, az F pont pedig a kocka DD 1 élének egyeneséhez tartozik. A pontok egy D 1 csúcsból kilépő egyenesekhez tartoznak.

A keresztmetszet egyenlő szárú trapézt eredményez, mivel F egyenlő távolságra van az A 1 u C 1 pontoktól, azaz LA 1 = KC 1 .

Egy D 1 csúcsú élekhez tartozó három pont. Az F u M pontok rendre a D 1 D u D 1 C élek folytatásaihoz tartoznak, az A 1 pont pedig a kocka csúcsa.

A keresztmetszet A 1 KLNG ötszöget eredményez.

Három F, M és Q pontot veszünk úgy, hogy a D 1 D, D 1 C 1, illetve D 1 A 1 élek folytatásán feküdjenek.

A keresztmetszet egy KLNGJH hatszöget eredményez.

Három pont olyan éleken fekszik, amelyeknek egy csúcsa D 1.

A keresztmetszet egy tetszőleges háromszöget eredményez, de ha a pontok úgy vannak elrendezve, hogy D 1 Q =D 1 M =D 1 F , vagyis ha egyenlő távolságra lennének a D 1 csúcstól, akkor a keresztmetszet adódik. egyenlő oldalú háromszögben.

A vágási síkot a H, Q és M pontok határozzák meg. A keresztmetszet egy paralelogrammát állít elő, mivel KC ││ MP és MK ││ PC a két párhuzamos sík egy harmadikkal való metszéspontjára vonatkozó tétel alapján.

Ha pont H, Q és M határozzuk meg a D-től távoli vágási síkot 2a távolságra, ahol a a kocka éle, akkor a metszetben egy ACB 1 szabályos háromszöget kapunk.

Következtetés: a metszetet meghatározó három pont a kocka három közös csúcsú éléhez tartozik, illetve ezek folytatása, ekkor a metszet eredménye: háromszög, ötszög, hatszög, trapéz, paralelogramma.

Egy kocka metszetének szerkesztése egy síkkal, ha három pont adott, amelyek közül kettő a szomszédos éleken, a harmadik pont pedig egy velük nem szomszédos élen fekszik.

Három pont M, K u F úgy vesszük, hogy M u F olyan élekhez tartozik, amelyeknek egy A 1 csúcsa van, és a K pont egy olyan élen van, amely nem szomszédos velük.

A keresztmetszet egy téglalapot eredményez, mivel A 1 M = D 1 K és három merőleges tételével igazolható, hogy az MKLF téglalap, és ha A 1 M D 1 K, akkor kaphat trapézt vagy ötszöget.

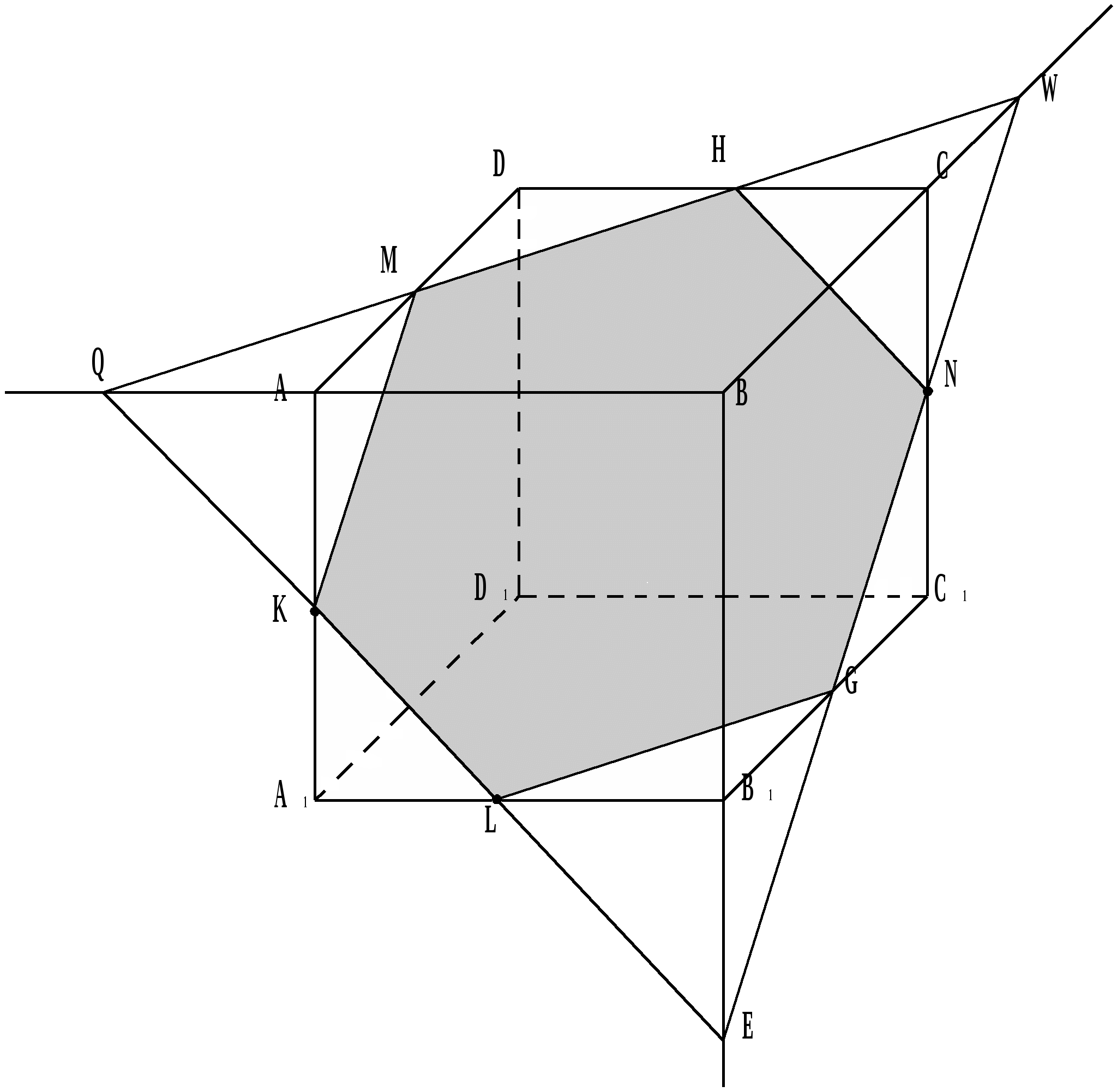
Három pontot veszünk úgy, hogy K u L az egyik A 1 csúcsból kilépő élekhez tartozik, az N pont pedig a CC 1 élhez tartozik, nem pedig szomszédos velük. Az A 1 A, A 1 B 1 u CC 1 élek felezőpontjainak K, L u N – ill.

A keresztmetszet szabályos KLGNHM hatszöget eredményez

Három pontot veszünk úgy, hogy K u L az egyik A 1 csúcsból kilépő élekhez tartozik, a T pont pedig a DC élhez tartozik.

A keresztmetszet hatszögletű KLFRTZ-t eredményez.

Három pontot veszünk úgy, hogy K u L a kocka egyik A 1 csúcsából származó éleihez, M pont pedig a DD 1 élhez tartozik.

A keresztmetszet trapéz alakú LKQM-et eredményez.

Három pont K u L amelyek egy A 1 csúcsú élekhez tartoznak, és egy R pont, amely a BC élen található.

A keresztmetszet egy KLFRT ötszöget eredményez.

Következtetés: Ha a vágási síkot három pont határozza meg, amelyek közül kettő a szomszédos éleken, a harmadik pedig egy velük nem szomszédos élen fekszik, akkor a metszet téglalapot, ötszöget, hatszöget, trapézt eredményezhet.

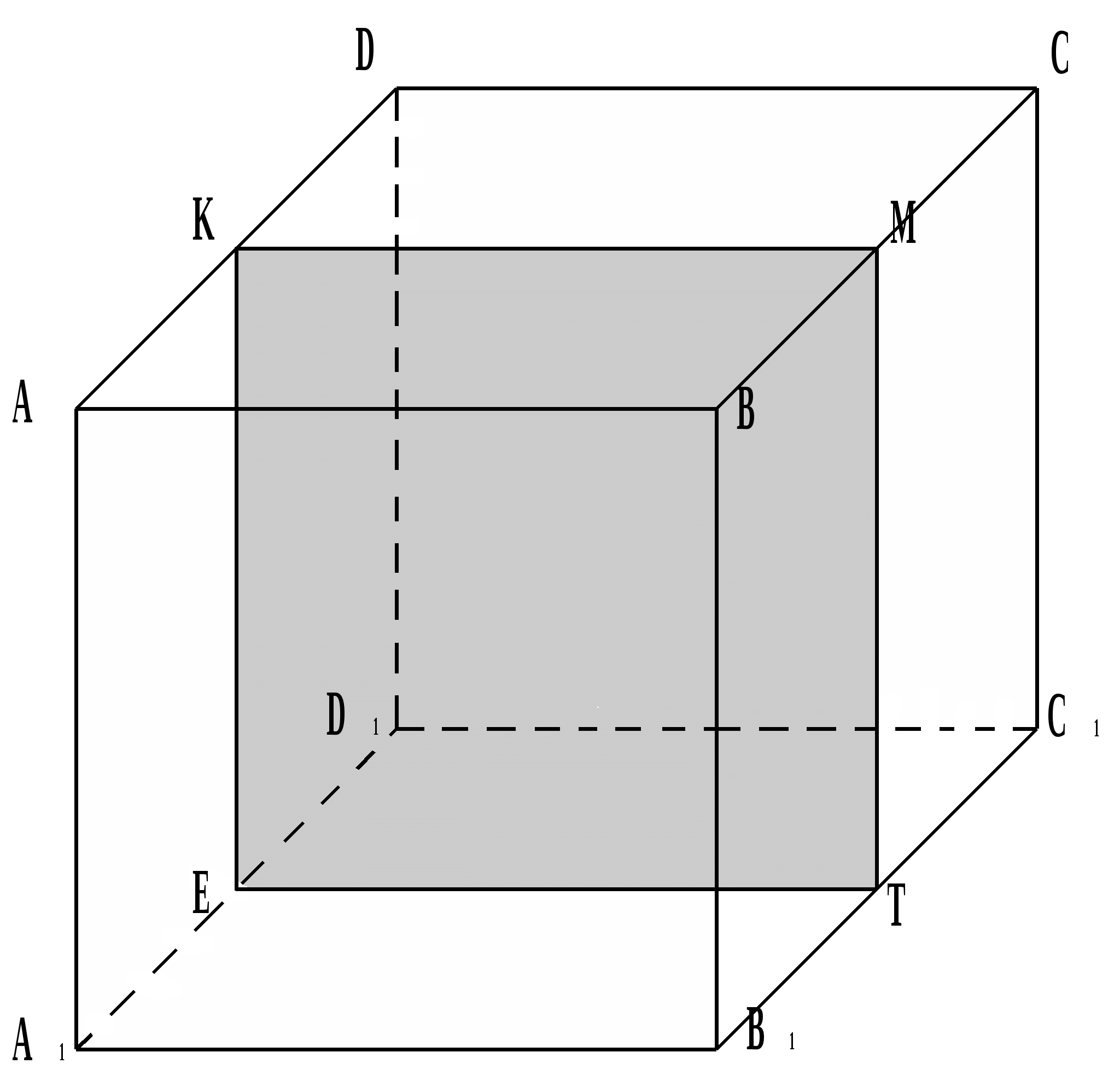
A kocka keresztmetszetében és speciális esetei paralelogramma található.

Pontok A szakaszt meghatározó T, H, J úgy helyezkednek el, hogy T.H. HIRDETÉS, H.J. HIRDETÉS. A keresztmetszet négyzetes HTKJ-t eredményez.

A szakaszt a C, F, L pontok határozzák meg, ahol DF = FD 1, BL = LB 1. A keresztmetszet egy rombusz AFCL-t hoz létre.

A szakaszt a C, G, H pontok határozzák meg. B 1 H = DG. A keresztmetszetben egy A 1 GCH paralelogramma található.

A szakaszt meghatározó pontok az A, D, C 1 kocka csúcsai. A keresztmetszet egy téglalapot eredményez

Szabályos sokszögek egy kocka keresztmetszetében

Az ABC 1 háromszög egyenlő oldalú, mivel oldalai a kocka lapjainak átlói.

A KMT háromszög egyenlő oldalú, mivel KV = MV = TV.

A KMTE négyzet, mivel a szakaszt az M, K, E és MK pontok határozzák meg HIRDETÉS, E.K. HIRDETÉS.

A szakasz szabályos hatszögű KMTNEO, mivel a szakaszt meghatározó H, E, K pontok a CC 1, DC, AA 1 élek felezőpontjai, ill.

Kocka és számos probléma a sztereometriával kapcsolatban az egységes államvizsgáról.

Az „Egységes államvizsga 2005. Matematika. Tipikus tesztproblémák” (Kornikova T. A. et al.) 10 sztereometriai feladatot (C4) tartalmaz, amelyeket egy közös ötlet egyesít: adott egy háromszög alakú ABCA prizma 1 BAN BEN 1 VAL VEL 1 az AB és BC alap oldalai egymásra merőlegesek és merőlegesek a BB élre 1 , AB=BC=BB 1 , az A csúcs a kúp teteje (vagy a henger egyik alapjának közepe, vagy a gömb közepe), a kúp alapja (a gömb vagy a henger második alapja) a közepén halad át a prizma egyik élének hossza ismert. Meg kell találnunk egy kúp (gömb, henger) térfogatát vagy felületét.

Általános példa megoldás:

Adja hozzá ezt a prizmát egy kockához. Hatszög DEFKLM - egy kocka egy kúp alapjának síkja szerinti metszete, amelynek köre átmegy a középső A 1 B 1, A a kúp csúcsa, ill.

A DEFKLM egy kocka egy henger alapjának síkjában lévő metszete, amelynek köre átmegy A 1 B 1 közepén, A a henger második talpának középpontja, vagy egy henger egy szakasza. kocka egy A középpontú gömb nagykörének síkjával, amelynek gömbje átmegy A 1 B 1 közepén.

HatszögDEFKLM– egy kocka metszete az A élek közepén átmenő síkkal 1 BAN BEN 1 , BB 1 , VSZh pontok megalkotásakorK, L, M, amelyek a megfelelő élek felezőpontjai. Ennek a hatszögnek az oldalai a háromszögek befogóiD.B. 1 E, EBF, FCK, KQL, LRM, M.A. 1 D, melynek lábai egyenlők a kocka élének felével. Ekkor ennek a hatszögnek a középpontja a körülötte körülírt kör középpontja, amely a kocka éleit pontokban metsziD, E, F, K, Lés M, ennek a körnek a sugara
, hol egy 1 BAN BEN 1 = A .

A.O. E.L. T. Nak nek. EAL – egyenlő szárú:AL = A.E. .

( ABE u EAL- téglalap alakú,AB= AQ= A, LENNI = L.Q. = )

EO =OL a DEFKLM hatszög EL átlójának felezőpontjaként, azaz AO a medián, és egy egyenlő szárú háromszög tulajdonságai szerint a magassága. Az AO-t hasonló módon bizonyítják DK. Mivel AO merőleges a hatszögsík két egymást metsző egyenesére, ezért AO merőleges a teljes síkra.

Ha A a kúp csúcsa, akkor AO a magassága, ha A a henger második alapjának közepe, akkor AO a henger magassága.

ABC: AC=
, P – a kocka alapjának átlóinak metszéspontjai, AP=
, RR 1 =AA 1 = A . VAGY=RR 1 = , majd a téglalapból ROA JSC=
. És így AO=
.

Akkor, ha kúpról beszélünk:

(tól től
).

Válasz:

Ha hengerről beszélünk:

Válasz:

Ha a gömbről beszélünk:

Válasz:

Kornikova T. A. és egyéb jellemző tesztfeladatok. Egységes államvizsga - 2005

6. lehetőség.

Feladat. Adott egy ABCA 1 B 1 C 1 prizma és egy henger. A prizma alapjának AB és BC oldalai merőlegesek a BB 1 élre, és egymásra merőlegesek. A henger alapjának középpontja az A 1 pont, a második alap köre az A 1 B 1 él közepén halad át.

Határozza meg a henger teljes felületét, ha BB 1 =AB=BC=10. Keresse meg a térfogatát.

Megoldás:

.
.

Óra témája: Feladatok szakaszok felépítéséhez.

Az óra célja:

Fejleszteni kell a tetraéder és a paralelogramma metszeteinek felépítésével kapcsolatos feladatok megoldási készségeit.

Az órák alatt

I. Szervezési mozzanat.

II. Házi feladat ellenőrzése

Válaszok a 14., 15. kérdésre.

14. Van olyan tetraéder, amelynek lapjai öt derékszögűek?

(Válasz: nem, mert csak 4 lap van, ezek háromszögek, és két derékszögű háromszög nem létezik.)

15. Van-e olyan paralelepipedon, amelynek: a) csak egy lapja van - egy téglalap;

b) csak két szomszédos rombuszlap; c) az arcok minden sarka éles; d) a lapok minden szöge egyenes; e) az összes éles él száma nem egyenlő a lapok összes tompaszögének számával?

(Válasz: a) nem (a szemközti oldalak egyenlőek); b) nem (azonos okból); c) nem (ilyen paralelogrammák nem léteznek); d) igen (téglalap alakú paralelepipedon); e) nem (mindegyik lapon két hegyes és két tompaszög van, vagy minden egyenes).

III. Új anyagok tanulása

Elméleti rész. Gyakorlati rész. Elméleti rész.

A tetraéderrel és a paralelepipedonnal kapcsolatos számos geometriai probléma megoldásához hasznos, ha metszeteiket különböző síkban tudjuk megrajzolni. Metszet alatt minden olyan síkot értünk (nevezzük vágósíknak), amelynek mindkét oldalán egy adott alakzat (tehát tetraéder vagy paralelepipedon) pontjai találhatók. A vágási sík szegmensek mentén metszi a tetraédert (paralleleppiped). A sokszög, amelyet ezek a szakaszok alkotnak, az ábra keresztmetszete. Mivel a tetraédernek négy lapja van, keresztmetszete lehet háromszög és négyszög. A paralelepipedonnak hat lapja van. Keresztmetszete lehet háromszög, négyszög, ötszög, hatszög.

A paralelepipedon metszetének elkészítésekor figyelembe vesszük, hogy ha egy vágósík egyes szakaszok mentén két egymással szemben lévő oldalt metsz, akkor ezek a szakaszok párhuzamosak (1. tulajdonság, 11. bekezdés: Ha két párhuzamos síkot egy harmadik, akkor metszéspontjuk egyenesei párhuzamosak).

A metszet elkészítéséhez elegendő a vágási sík metszéspontjait a tetraéder éleivel (paralleleppiped) megszerkeszteni, majd megrajzolni az ugyanazon a lapon fekvő két konstruált pontot összekötő szakaszokat.

Vágható-e tetraéder síkkal az ábrán látható négyszögbe?

https://pandia.ru/text/78/630/images/image002_130.gif" width="626" height="287 src=">

2.2. Szerkesszünk meg egy kocka szakaszt a pontokon átmenő síkkal E, F, G, a kocka szélein fekve.

E, F, G,

csináljunk közvetlen E.F.és jelöljük P a metszéspontjával HIRDETÉS.

Jelöljük K vonalak metszéspontja PGÉs AB.

Kössük össze a pontokat EÉs K, FÉs G.

A kapott trapéz EFGQ lesz a kívánt szakasz.

https://pandia.ru/text/78/630/images/image004_91.gif" width="624" height="287">

2.4. Szerkesszünk meg egy kocka szakaszt a pontokon átmenő síkkal E, F, a kocka és a csúcs szélein fekszik B.

Megoldás. Egy kocka pontokon átmenő szakaszának megalkotása E, Fés a felső B,

Kössük össze a pontokat szegmensekkel EÉs B, FÉs B.

Pontokon keresztül EÉs F húzzunk párhuzamos egyeneseket B.F.És LENNI, ill.

A kapott paralelogramma BFGE lesz a kívánt szakasz.

2.5. Szerkesszünk meg egy kocka szakaszt a pontokon átmenő síkkal E, F, G, a kocka szélein fekve.

Megoldás. Egy kocka pontokon átmenő szakaszának megalkotása E, F, G,

csináljunk közvetlen E.F.és jelöljük P a metszéspontjával HIRDETÉS.

Jelöljük K,R vonalmetszéspontok PG Val vel ABÉs DC.

Jelöljük S metszéspont FR c SS 1.

Kössük össze a pontokat EÉs K, GÉs S.

A kapott ötszög EFSGQ lesz a kívánt szakasz.

2.6. Szerkesszünk meg egy kocka szakaszt a pontokon átmenő síkkal E, F, G, a kocka szélein fekve.

Megoldás. Egy kocka pontokon átmenő szakaszának megalkotása E, F, G,

találjunk egy pontot P egy egyenes metszéspontja E.F.és az arc síkja ABCD.

Jelöljük K, R vonalmetszéspontok PG Val vel ABÉs CD.

Csináljunk direkt RFés jelöljük S, T metszéspontjaival CC 1 és DD 1.

Csináljunk direkt T.E.és jelöljük U a metszéspontjával A 1D 1.

Kössük össze a pontokat EÉs K, GÉs S, F és U.

A kapott hatszög EUFSGQ lesz a kívánt szakasz.

2.7. Szerkesszük meg a tetraéder keresztmetszetét! ABCD HIRDETÉSés áthalad a pontokon E, F.

Megoldás. Kössük össze a pontokat EÉs F. A ponton keresztülF húzzunk egy egyenestFG, párhuzamosHIRDETÉS.

Kössük össze a pontokat GÉs E.

A kapott háromszög EFG lesz a kívánt szakasz.

2.8. Szerkesszük meg a tetraéder keresztmetszetét! ABCDélével párhuzamos sík CDés áthalad a pontokon E, F .

Megoldás. Pontokon keresztül EÉs F húzzunk egyenes vonalakat PÉLDÁUL.És FH, párhuzamos CD.

Kössük össze a pontokat GÉs F, EÉs H.

A kapott háromszög EFG lesz a kívánt szakasz.

2.9. Szerkesszük meg a tetraéder keresztmetszetét! ABCD pontokon áthaladó sík E, F, G.

Megoldás. Pontokon átmenő tetraéder szakasz megszerkesztése E, F, G,

csináljunk közvetlen E.F.és jelöljük P a metszéspontjával BD.

Jelöljük K vonalak metszéspontja PGÉs CD.

Kössük össze a pontokat FÉs K, EÉs G.

A kapott négyszög EFQG lesz a kívánt szakasz.

IV. Óra összefoglalója.

V. Házi feladat 14. o., 27. o. 000. sz. – 1., 2. lehetőség.